Solveeit Logo
Login

Question

Question: A spring is stretched 2 cm when a mass of 40 grams is hung from it. What is the spring constant of t...

A spring is stretched 2 cm when a mass of 40 grams is hung from it. What is the spring constant of the spring?

Explanation

Solution

In order to solve the question, we will first convert the mass and the starched length into their standard international unit that is kilogram and meter respectively then we will make then free body diagram which will help us to equate the force so that we can solve for spring constant.

Formula Used:
F = Kx
F = force
K = spring constant
x = stretched length
F = mg
m = mass
g is acceleration by gravity

Complete step by step answer:
In the question we are given a spring which is stretched with a mass hung from it and we have to find the spring constant of the spring
Length up to which spring is stretched = 2 cm
Mass which is hung to spring = 40 g
For solving further, we will first convert the mass from gram to kilogram
1g = 11000kg\dfrac{1}{{1000}}kg
Which means 1 g = 10−3kg{10^{ - 3}}kg
Now we will convert grams into for the given question
40 g = 40×10−3kg40 \times {10^{ - 3}}kg
We also have to convert centimetre into meter for stretched length
1 cm = 1100cm\dfrac{1}{{100}}cm
Which means 1 cm = 10−2m{10^{ - 2}}m
Now we will convert grams into for the given question
2 cm = 2×10−2m2 \times {10^{ - 2}}m
Now we will make the free body diagram of the given scenario

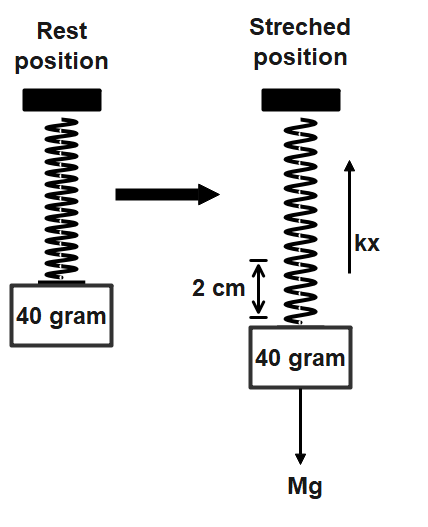
The spring applies the force when it is stretched in order to maintain the action for the reaction of pulling the formula of the spring force which stretches back is
F = Kx
From the free body diagram, we can conclude that force applied against spring force is gravitational force caused by the mass
Mg = Kx
Now we will substitute the value of M that is mass, g that is constant (where g = 9.8 ms−2m{s^{ - 2}}) and x that is stretched length
40×10−3kg×9.8 ms−2=2×10−2m×K40 \times {10^{ - 3}}kg \times 9.8{\text{ }}m{s^{ - 2}} = 2 \times {10^{ - 2}}m \times K
Solving for spring constant
K=40×10−3kg×9.8 ms−22×10−2m=19.6Nm−1K = \dfrac{{40 \times {{10}^{ - 3}}kg \times 9.8{\text{ }}m{s^{ - 2}}}}{{2 \times {{10}^{ - 2}}m}} = 19.6N{m^{ - 1}}
Hence, the answer is K=19.6 Nm−1K = 19.6{\text{ }}N{m^{ - 1}}.

Note: Many of the people will may use the acceleration caused by gravity as g = 10 ms−2m{s^{ - 2}}but it can be only taken as 10 ms−2m{s^{ - 2}}when it is given in the question otherwise as standards it will be 9.8 ms−2m{s^{ - 2}}and the spring constant is in newton upon meter because that is the most popular SI unit for spring constant. instead of kg upon second square