Question

A spring is compressed between two toy-carts of masses $m_1$ and $m_2$ .When the toy-carts are released, the spring exerts on equal and opposite average forces for the same time $t$. It the coefficient of friction $\mu$ between the ground and the carts are equal, then the displacements of the two toy-carts are in the ratio-
A. $\dfrac{{S_1}}{{S_2}} = \dfrac{{m_2}}{{m_1}}$
B. $\dfrac{{S_1}}{{S_2}} = \dfrac{{m_1}}{{m_2}}$
C. $\dfrac{{S_1}}{{S_2}} = - {\left( {\dfrac{{m_2}}{{m_1}}} \right)^2}$
D. $\dfrac{{S_1}}{{S_2}} = - {\left( {\dfrac{{m_1}}{{m_2}}} \right)^2}$

Answer 1

First draw a rough diagram with help of the given statement. Assume two different distances travelled by the two carts in opposite directions. We know the formula for the force of friction and the kinetic energy formula of a body. Equating the work done by the carts and kinetic energy of the carts. After that, find the ratio of that distance.

Complete step by step answer:
As per the given problem, a spring is compressed between two toy-carts of masses $m_1$ and $m_2$ .When the toy-carts are released, the spring exerts on equal and opposite average forces for the same time $t$. The coefficient of friction $\mu$ between the ground and the carts are equal.We need to calculate the ratio of displacements of the two toy-carts

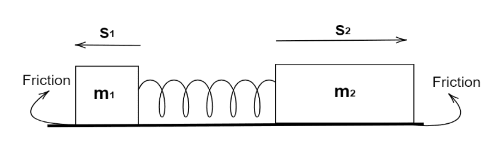
Let us assume $S_1$ and $S_2$ be the displacement of the two carts respectively moving in the opposite direction to that of the spring compression.And let $m_1$ and $m_2$ be the mass of the two carts respectively and the coefficient of friction $\mu$ between the ground and the carts are equal.

Case I: When the displacement is $S_1$. We know the frictional force on $m_1$ be,
$f_1 = \mu m_1g$
Where, the coefficient of friction is equal to $\mu$ and Mass of the toy-card is equal to $m_1$.
Now the work done by the frictional force is equal to,
Work done = Frictional Force multiplied with Displacement
$W_1 = f_1 \times S_1$
Now putting $f = \mu m_1g$ , we will get
$W_1 = \mu m_1g \times S_1$

The initial kinetic energy of the toy is,
$KE_1 = \dfrac{{{p^2}}}{{2m_1}}$
Where,
Momentum = p
Now by using conservation of mechanical energy we will get,
$W_1 = KE_1$
Now putting the respective value we will get,
$\mu m_1g \times S_1 = \dfrac{{{p^2}}}{{2m_1}}$
Rearranging the above terms we will get,
$S_1 = \dfrac{{{p^2}}}{{2m_1\left( {\mu m_1g} \right)}}$
$\Rightarrow S_1 = \dfrac{{{p^2}}}{{2{m_1}^2\mu g}} \ldots \ldots \left( 1 \right)$

Case II: When the displacement is $S_2$. We know the frictional force on $m_1$ be,
$f_2 = \mu m_2g$
Where, The coefficient of friction is equal to $\mu$ and Mass of the toy-card is equal to $m_1$.
Now the work done by the frictional force is equal to,
Work done = Frictional Force multiplied with Displacement
$W_2 = f_2 \times S_2$

Now putting $f = \mu m_1g$ , we will get
$W_2 = \mu m_2g \times S_2$
The initial kinetic energy of the toy is,
$KE_2 = \dfrac{{{p^2}}}{{2m_2}}$
Where, Momentum = p
Now by using conservation of mechanical energy we will get,
$W_2 = KE_2$
Now putting the respective value we will get,
$\mu m_2g \times S_2 = \dfrac{{{p^2}}}{{2m_2}}$
Rearranging the above terms we will get,
$S_2 = \dfrac{{{p^2}}}{{2m_2\left( {\mu m_2g} \right)}}$
$\Rightarrow S_2 = \dfrac{{{p^2}}}{{2{m_2}^2\mu g}} \ldots \ldots \left( 2 \right)$

For the two carts the momentum is numerically same, the coefficient of friction is also same as given in the problem itself and the gravitational constant is the universal constant term.
Now taking the ratio of equation $\left( 1 \right)$ is to $\left( 2 \right)$ we will get,
$\dfrac{{S_1}}{{S_2}} = \dfrac{{\dfrac{{{p^2}}}{{2{m_1}^2\mu g}}}}{{\dfrac{{{p^2}}}{{2{m_2}^2\mu g}}}}$
Cancelling the constant terms we will get,
$\dfrac{{S_1}}{{S_2}} = \dfrac{{\dfrac{1}{{{m_1}^2}}}}{{\dfrac{1}{{{m_2}^2}}}}$
$\Rightarrow \dfrac{{S_1}}{{S_2}} = \dfrac{{{m_2}^2}}{{{m_1}^2}}$
As they are moving the the opposite direction the ratio become,
$\dfrac{{S_1}}{{S_2}} = - \dfrac{{{m_2}^2}}{{{m_1}^2}}$

Therefore the correct option is $\left( C \right)$.

Note: Always remember if you take displacement as negative from the very beginning then no need to do the last steps. The momentum of the two bodies is the same as the spring exerts maximum compression then the conservation of linear momentum takes place and both the bodies move at the same velocity.