Question

A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is $2N{m^{ - 1}}$ and the mass of the block is $2kg$. Ignore the mass of the spring. Initially, the spring is in an unstretched condition. Another block of mass $1kg$ moving with a speed of $2m{s^{ - 1}}$ collides elastically with the first block. The collision is such that the $2kg$ block does not hit the wall. The distance, in metres between the two blocks when the spring returns to its unstretched position for the first time after the collision is _______.

Answer 1

The spring constant is given by the Hooke’s law. The Hooke’s law provides the force exerted by a spring on an object attached to it. Mathematically, it is expressed as,
$F = - kx$
Here, F is the force exerted by the spring on an object attached to it, k is the spring constant and x is the distance by which the spring has been stretched or compressed from its rest position. The spring constant, k is the measure of stiffness and strength of a spring. In this problem, the value of spring constant is already provided. In order to solve the problem, we need to first calculate the velocities of the $1$ Kg and $2$ Kg block after collision between the two and then solve for the time period of the given spring followed by calculating the distance.

Formula Used:
The following formula we will use to calculate the distance as mentioned in question:
$d = \dfrac{2}{3}\pi$
Here, d represents the distance in metres between the two blocks on returning of spring to its unstretched position for the first time after the collision and $\pi$ is a mathematical constant with value of 3.14.

Complete step by step answer:
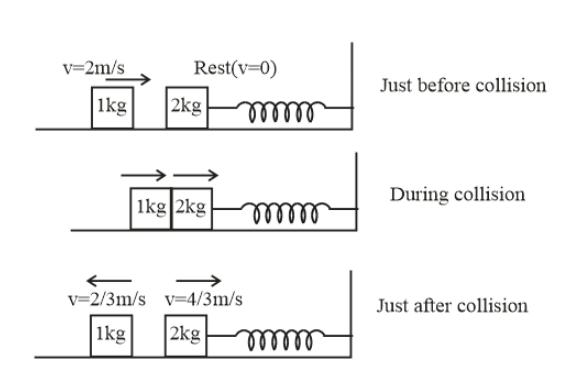
Given masses of block A is $1$ Kg and that of block B is$2$ Kg. Also speed of block A is ${u_A} = 2m{s^{ - 1}}$ and that of block B is ${u_B} = 0$
Now in the x-direction the momentum is conserved hence we can find the speeds of the blocks just after collision by the following momentum conservation formula. We should also note that the rate of change of momentum is the net force acting on the system in a particular direction.
Hence, after collision their respective speeds will be-
${v_B} = \dfrac{{2 \times 2}}{{2 + 1}} \\\ \Rightarrow{v_B} = \dfrac{4}{3}m{s^{ - 1}} \\\ \Rightarrow{v_A} = \dfrac{2}{{2 + 1}} = \dfrac{2}{3}m{s^{ - 1}} \\\$
Speed of B will be towards right and speed of A will be towards left. If we show by diagram we have-

Now the time period of the spring will be,
$T = 2\pi \sqrt {\dfrac{m}{k}}$, here the spring constant K is $2N{m^{ - 1}}$ and the mass of block B is $2$ Kg.
The above formula is the representation of the period of mass m on spring with spring constant k.
So we can get the time period for the first oscillation which will be,
$T = 2\pi \sqrt {\dfrac{m}{k}}$
$\Rightarrow T = 2\pi \sqrt {\dfrac{2}{2}} \\\ \Rightarrow T= 2\pi$
So, the halfway path will be travelled by the block B in $\dfrac{T}{2} = \pi$
That means the block returns to the original position in $\pi$ seconds.
Now the distance travelled will be
$\Rightarrow d = \dfrac{2}{3}\pi$
$\therefore d = \dfrac{2}{3}\left( {3.14} \right) = 2.0933$

The required distance value is approximately $2.09$ m.

Note: In the above problem, the effect due to friction between the blocks and ground is not considered. If the friction effect would have been considered, then the momentum would not have been conserved and the values of the speeds would have been different.