Question
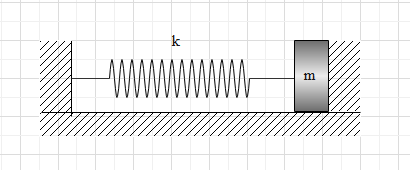
Question: A spring block system is placed on a horizontal surface so as to just fit within the vertical walls....
A spring block system is placed on a horizontal surface so as to just fit within the vertical walls. The spring is initially unstretched. The coefficient of restitution for collision is e=21 . The block is pulled to the left by a distance x=1cm and released from rest. The time between second and third collision of the block with the wall is
A. 2πkm
B. πkm
C. 2πkm
D. 4πkm
Solution
Hint-
Coefficient of restitution for an object colliding with a perfectly rigid wall is defined as the ratio of final velocity to initial velocity or the speed of separation to speed of approach
Therefore,
e=vavs=21
Where,vs is the velocity of separation,va is the velocity of approach
Time period in simple harmonic motion is independent of the amplitude. It is given by the equation,
T=2πkm
Where, m is the mass and k is the spring constant.
Coefficient of restitution is given as21 . It means that velocity becomes twice in second collision
Since velocity and time are inversely related. The time becomes 21
That is, time for second oscillation
t=2T
Complete step-by-step answer:
Given,
Coefficient of restitution for collision is , e=21
Coefficient of restitution for an object colliding with a perfectly rigid wall is defined as the ratio of final velocity to initial velocity or the speed of separation to speed of approach
Therefore,
e=vavs=21
Where, vs is the velocity of separation, va is the velocity of approach.
When the block strikes the wall, it bounces back because of the normal reaction exerted by the wall
The motion here is simple harmonic motion.
A simple harmonic motion is a periodic motion in which the restoring force is directly proportional to the displacement and acting towards the equilibrium position
Time period in simple harmonic motion is independent of the amplitude. It is given by the equation,
T=2πkm
Where, m is the mass and k is the spring constant.
Since, the coefficient of restitution is given as 21. It means that velocity becomes twice in a second collision.
Since velocity and time are inversely related. The time becomes 21
That is, time for second oscillation,
t=2T
Therefore,
So, the correct answer is option B.
Note:
Formulas to remember-
T=2πkm
Where, T is the time period in simple harmonic motion, m is the mass and k is the spring constant.
Coefficient of restitution for collision,
e=vavs
Where, vs is the velocity of separation, va is the velocity of approach.
