Question

A spring balance and a physical balance are kept in a lift. In these balances equal masses are placed. What will happen if now the lift starts moving upwards with constant acceleration?
${\text{A}}{\text{.}}$ The reading of spring balance will increase and the equilibrium position of the physical balance will disturb
${\text{B}}{\text{.}}$ The reading of spring balance will remain unchanged and physical balance will remain in equilibrium
${\text{C}}{\text{.}}$ The reading of spring balance will decrease and physical balance will remain in equilibrium
${\text{D}}{\text{.}}$ The reading of spring balance will increase

Answer 1

Here, we will proceed by making the free body diagram of all the bodies in the system along with the consideration of the pseudo force which will be acting on the masses placed in the lift.

Complete answer:
Let us suppose that a spring balance with a block of mass M is placed in a lift (initially at rest and then started moving upwards with a constant acceleration ‘a’) as shown in the figure. In this same lift, a physical balance with a block B of mass ${{\text{M}}_{\text{B}}}$ is placed in one pan and a block of mass M is placed in the other pan.

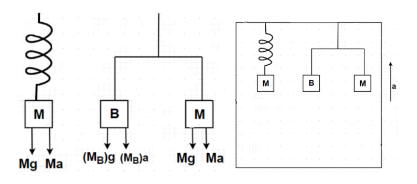
In spring balance, the mass hanging will experience a spring force and the gravitational force acting. Initially when the lift will be at rest, the spring force acting on the mass M will be equal to the gravitational force acting on the mass M. This is used to get the reading of the spring balance. In the reading of any spring balance, the weight of the mass hanging is represented.
Initially, there is no pseudo force acting on the masses hanging in the spring balance so the reading of the spring balance will be Mg (the weight of the mass M).

In physical balance, the mass whose weight is required (here it is M) is balanced by placing another mass in the other pan such that these two masses are equal so that the set up can be balanced. In the reading of any physical balance, the weight of the mass (required) which is hanged is shown.
Initially, there is no pseudo force acting on the masses hanged in the physical balance, so the reading of the physical balance will be in equilibrium (because ${\text{M}} = {{\text{M}}_{\text{B}}}$).

As the lift starts moving in the upward direction with a constant acceleration ‘a’, pseudo forces will act on the masses.
In spring balance, the block of mass M hanging will experience two forces i.e., gravitational force (Mg) and pseudo force (Ma). The total force acting on the block will be Mg+Ma = M(g+a). This will be balanced by the spring force. So, the apparent weight of the block hanging in the spring balance will increase and hence, the reading of the spring balance will also increase.

In physical balance, both the balanced block of mass ${{\text{M}}_{\text{B}}}$ and block of mass M will experience pseudo force. The total force acting on the balanced block will be $\left( {{{\text{M}}_{\text{B}}}} \right){\text{g}} + \left( {{{\text{M}}_{\text{B}}}} \right){\text{a}} = {{\text{M}}_{\text{B}}}\left( {{\text{g}} + {\text{a}}} \right)$ and the total force acting on the mass M will be Mg+Ma = M(g+a).
Since, for equilibrium ${\text{M}} = {{\text{M}}_{\text{B}}} \Rightarrow {\text{M}}\left( {{\text{g}} + {\text{a}}} \right) = {{\text{M}}_{\text{B}}}\left( {{\text{g}} + {\text{a}}} \right)$
i.e., Force acting on the mass M = Force acting on the balanced mass
The above equation represents that there will be no change in the equilibrium position of the physical balance.
Therefore, the reading of spring balance will increase and the physical balance will remain in equilibrium.

So, the correct answer is “Option D”.

Note:
A spring balance is simply a type of weighing scale used to find the weight of an object. This type of balance works on the Hooke’s law. According to Hooke’s law, force required to elongate or compress is directly proportional to the amount of the elongation or compression occurred in the spring.