Question

A spring 40mm long is stretched by the application of a force. If 10N force required to stretch the spring through 1mm, then work done in stretching the spring through 40mm is:

Answer 1

The spring constant is constant for any given spring and is denoted by $k$.It is the force required to change to length from the natural length of the spring by one unit. And the Work Done is given by the Formula given below.

Formula used:
$k=\dfrac{F}{x}$
$W=\dfrac{1}{2}k{{x}^{2}}$

Complete step-by-step answer:
In the stretching and contraction of any spring Work has to be done. This work is proportional to the spring constant of the spring and the square of the change of length from the natural length of the spring. The spring constant is constant for any given spring and is denoted by $k$.It is the force required to change to length from the natural length of the spring by one unit. It can be formularised as
$k=\dfrac{F}{x}$
Coming to the question, the force required to make a change of 1mm length is given.
$F=10N$
And the change in length is also given, 1mm or 0.001 m

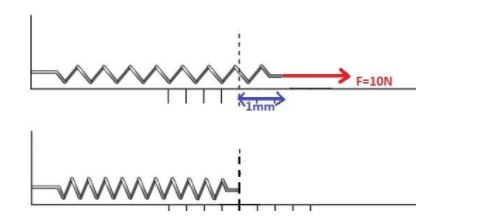
From the given information we can find the spring constant of the spring

& k=\dfrac{F}{x} \\\ & \Rightarrow k=\dfrac{10}{0.001} \\\ & \Rightarrow k=1\times {{10}^{4}}N/m \\\ \end{aligned}$$ So the spring constant of the spring is $$k=1\times {{10}^{4}}N/m$$ Now we need to find the work done in stretching the spring. This work is proportional to the spring constant of the spring and the square of the change of length from the natural length of the spring. $$W=\dfrac{1}{2}k{{x}^{2}}$$ We need x in the standard unit. $$\begin{aligned} & x=40mm \\\ & \Rightarrow x=\dfrac{40}{1000}m \\\ \end{aligned}$$ Plugging in the Values $$\begin{aligned} & W=\dfrac{1}{2}k{{x}^{2}} \\\ & \Rightarrow W=\dfrac{1}{2}\times {{10}^{4}}\times {{\left( \dfrac{40}{1000} \right)}^{2}} \\\ & \Rightarrow W=\dfrac{1}{2}\times {{10}^{4}}\times \dfrac{16}{{{10}^{4}}} \\\ & \Rightarrow W=8J \\\ \end{aligned}$$ Work done in stretching the spring through 40mm is 8 Joules. **Note:** The force required to stretch or compress a spring is directly proportional to the stretch or the compress. This is called Hooke’s Law and the work done and potential energy of the spring is derived from this Law only. Hooke’s Law is formularised as $$F=kx$$.