Question
Question: A spot of light S rotates in a horizontal plane with a constant angular velocity of 0.1rad/s. The sp...
A spot of light S rotates in a horizontal plane with a constant angular velocity of 0.1rad/s. The spot of light P moves along the wall at a distance of 3m from S. The velocity of spot P, where θ=45∘ , is?
A. 0.5m/s
B. 0.6m/s
C. 0.7m/s
D. 0.8m/s
Solution
Hint:- The formula for angular velocity is given by ω=dtdθ where θ is the angle between the perpendicular from the source to the wall and the line joining the source and the spot. For your better understanding a diagram is given for the situation.
Complete step-by-step solution:-
The situation in the question is given in the diagram for better understanding
As given in the question that the perpendicular distance between the source and the wall, SA=r=3m
Let angle between SA and SP be θ and the distance PA be x
Now, the velocity of the spot of light P, v is the rate at which x is changing i.e. v=dtdx
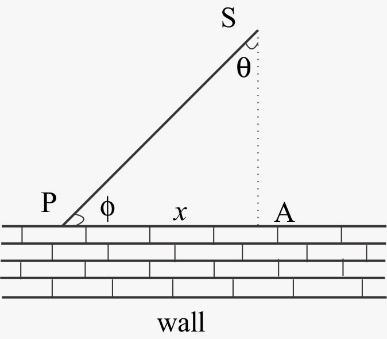
As from figure,
x=rtanθ
So, velocity of the point P
v=dtdx=rsec2θdtdθ
Now as we know that angular velocity is given by ω=dtdθ where θ is the angle between the perpendicular from the source to the wall and the line joining the source and the spot.
So, the equation becomes v=rωsec2θ
Now according to the question θ=45∘ , r=3m and angular velocity ω=0.1rad/s
So, substituting these value in the above equation, we have
v=3×0.1×sec245∘=3×0.1×2
So, v=0.6m/s
Hence option B is correct.
Note:- Angular velocity is the time rate of change of angular displacement at which an object or a particle is rotating around a center or a specific point. It is also known as rotational velocity. The unit of Angular velocity is angle per unit time or radians per second (rad/s). The rate of change of angular velocity is angular acceleration.
Angular velocity plays an important role in the rotational motion of an object. The linear velocity of every particle of a body in circular motion is directly related to the angular velocity of the whole object.
