Question

A spot light S moves in a horizontal plane with a constant angular velocity of $0.1rad/s$. The spot light P moves along the wall at a distance $3m$. When $\theta =45{}^\circ$, the velocity of spot P is?

Answer 1

The rotating spot light has an angular velocity and linear velocity. These two velocities are proportional to each other. Their relationship can be expressed in terms of distance, and angle between the center and angle of rotation. The angle, distance from spotlight to wall and angular velocity of spotlight are given in the question. We can derive the result from the formula for linear velocity.

Formula used:
$v=\dfrac{\omega r}{{{\sin }^{2}}\theta }$
$r=\dfrac{d}{\cos \theta }$

Complete answer:

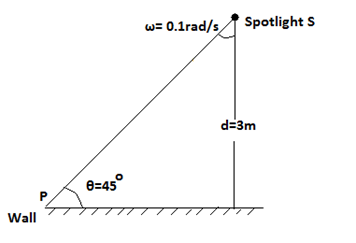
Here, a spot light S is moving horizontally along the wall with an angular velocity of $0.1rad/s$. Distance to the wall is $3m$. It makes an angle $\theta =45{}^\circ$ at a point.
Linear velocity of rotating object is given by,
$v=\dfrac{\omega r}{{{\sin }^{2}}\theta }$ ---------- 1
Where,
$\omega$ is the angular velocity
$r$ is the distance from the center
$d$ is the distance from the spotlight to wall,
We have,
$r=\dfrac{d}{\cos \theta }$
Given,
$d=3m$
$\theta =45{}^\circ$
Then, the distance from the spot of the light from the center at an angle $45^\circ$ is
$r=\dfrac{d}{\cos \theta }=\dfrac{3}{\cos 45}=3\sqrt{2}$
$r=3\sqrt{2}$
Given,
$\omega =0.1g rad/s$
Substitute the values of $\omega$, r and $\theta$ in equation 1. We get,
$v=\dfrac{0.1\left( 3\sqrt{2} \right)}{\sin 45}=0.6m/s$
Therefore, answer is $\text{v = 0}\text{.6m/s}$

Additional Information:
The rate of change of angular displacement is known as the angular velocity. It has the unit in $rad/s$. When objects rotate about some axis, each point in the object follows a circular arc. Every point on the rotating object has the same angular velocity. The tangential velocity of each point is proportional to its distance from the axis of rotation.

Note:
The expression, $v=\omega \times r$ is valid only if $\omega$ and r are in the same plane. A unit circle has radius as 1 unit. Hence, in this case linear velocity and angular velocity of an object is the same.