Question

A spool of mass $M$, inner radius $R$ and outer radius $2R$ is released from rest from the position as shown in figure. If moment of inertia of spool about its central axis is $\frac{5}{4}MR^2$, then at this instant.

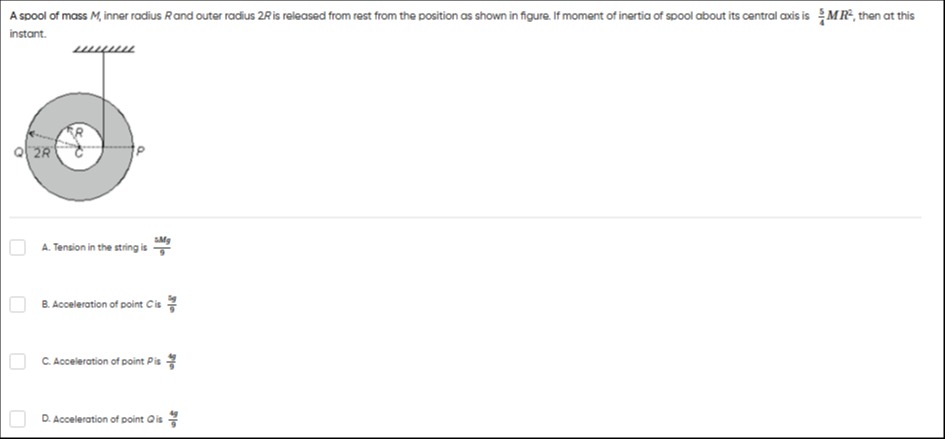
• A. Tension in the string is $\frac{5Mg}{9}$
• B. Acceleration of point C is $\frac{5g}{9}$
• C. Acceleration of point P is $\frac{4g}{9}$
• D. Acceleration of point Q is $\frac{4g}{9}$

Answer 1

Answer: (A), (D)

A, D

Answer 2

Assuming the string is wound around the inner radius $R$ and the spool unwinds. Forces: Gravity ($Mg$) down, Tension ($T$) up. Torque about center C: $TR$ (assuming unwinding to the left). Equations of motion:

1. Translation: $Mg - T = Ma$
2. Rotation: $TR = I\alpha$ Kinematic constraint: $a = R\alpha$ Given $I = \frac{5}{4}MR^2$. Substitute $I$ into the rotational equation: $TR = \frac{5}{4}MR^2\alpha \implies T = \frac{5}{4}MR\alpha$. Substitute $a=R\alpha$ into the translational equation: $Mg - T = MR\alpha$. Substitute $T = \frac{5}{4}MR\alpha$: $Mg - \frac{5}{4}MR\alpha = MR\alpha \implies Mg = \frac{9}{4}MR\alpha \implies \alpha = \frac{4g}{9R}$. Acceleration of center C: $a = R\alpha = R\left(\frac{4g}{9R}\right) = \frac{4g}{9}$ downwards. Tension: $T = \frac{5}{4}MR\alpha = \frac{5}{4}MR\left(\frac{4g}{9R}\right) = \frac{5Mg}{9}$. Acceleration of point Q (on outer rim, opposite to P): $\vec{a}_Q = \vec{a}_C + \vec{a}_{Q/C}$ $\vec{a}_C$ is downwards with magnitude $\frac{4g}{9}$. $\vec{a}_{Q/C}$ is tangential acceleration of Q relative to C, magnitude $(2R)\alpha = 2R\left(\frac{4g}{9R}\right) = \frac{8g}{9}$. Since Q is to the left and rotation is counter-clockwise, $\vec{a}_{Q/C}$ is upwards. $a_Q = a_C - (2R)\alpha = \frac{4g}{9} - \frac{8g}{9} = -\frac{4g}{9}$. The negative sign means upward acceleration. So, $a_Q = \frac{4g}{9}$ upwards. Option A is correct. Option D is correct.