Question

A spool of inner radius R and outer radius 3R has a moment of inertia $=M{{R}^{2}}$about an axis passing through its geometric center, where M is the mass of the spool. A thread wound on the inner surface of the spool is pulled horizontally with a constant force $=Mg$. Find the acceleration of the point on the thread which is being pulled assuming that the spool rolls purely on the floor.

Answer 1

We will first equate the torques acting on the spool about the center of rotation. Then by making use of parallel axis theorem we find the moment of inertia and obtain a relation between them. Substitute acceleration of center of mass in the angular acceleration formula, we can find the required answer.

Formula used: $MgR=I\alpha$

Complete step by step answer:
The free body diagram of spool is given below

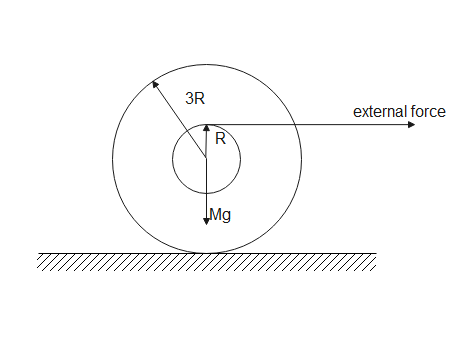
The external radius of the spool is R and internal radius is R.
Gravitational force acts on the body Mg in the download direction.
Now, let us equate the torques acting on the spool about the instantaneous center of rotation$Mg(3R+R)=I\alpha$
Where I is the moment of inertia of the spool and $\alpha$is the angular acceleration.
$\Rightarrow Mg(4R)=I\alpha \text{ }............\text{(1)}$
We will now use the parallel axis theorem, moment of inertia about the instantaneous center
$I=M{{R}^{2}}+M{{(3R)}^{2}}=10M{{R}^{2}}$
Substituting in equation (1) we get
$\Rightarrow 4MgR=10M{{R}^{2}}\alpha$
$\Rightarrow 4g=10R\alpha \text{ }...........\text{(2)}$
Now, we can write in terms of acceleration ‘a’ and radius
$\alpha =\dfrac{a}{3R}$
So, equation (2) becomes
$\begin{aligned} & 4g=10R\times \dfrac{a}{3R} \\\ & \Rightarrow 4g=\dfrac{10a}{3} \\\ & \therefore a=\dfrac{12g}{10} \\\ \end{aligned}$
Here, a is the acceleration of the center of mass.
Thus, the acceleration of the thread ${{a}_{t}}$​ is given by the acceleration of a point at a distance R from the center or 4R from the instantaneous axis.
$\begin{aligned} & {{a}_{t}}=4R\alpha \\\ & \Rightarrow {{a}_{t}}=4R\dfrac{a}{3R} \\\ & \Rightarrow {{a}_{t}}=\dfrac{4}{3}a \\\ & \Rightarrow {{a}_{t}}=\dfrac{4}{3}\times \left( \dfrac{12}{10}g \right) \\\ & \therefore {{a}_{t}}=\dfrac{16}{10}g \\\ & \therefore {{a}_{t}}=16m/{{s}^{2}} \\\ \end{aligned}$

Therefore, the acceleration of the point on the thread which is being pulled is $16m/{{s}^{2}}$

Note: Moment of inertia expresses a body's tendency to resist angular acceleration. It is equal to the “sum of the product of mass” of each particle with the “square of its distance from the axis of the rotation”. The formula for moment of inertia is
$I=\sum{{{m}_{i}}}{{r}_{i}}^{2}$.