Question

A spherically symmetric gravitational system of particles has a mass density
\rho = \left\\{ {\rho _0},r \leqslant R \\\ \,\,\,\,\,\,\,\,\,\,\,0,r > R \right\\}
where ${\rho _0}$ is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed V as a function of distance $r(0 < r < \infty )$ from the centre of the system is represented by.
A.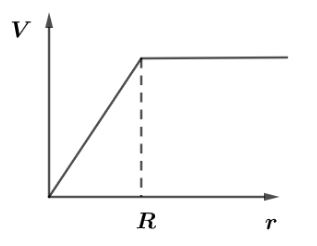
B.
C.
D.

Answer 1

In order to solve this question, we will first balance the centripetal force acting on a test mass with the gravitational force due to sphere and then will figure out the relation between velocity and distance and then choose the correct graph of velocity and distance.

Formula Used:
If $M$ and $M’$ be the mass of two bodies and r is the distance between them then, gravitational force of attraction between them is,
${F_G} = G\dfrac{{MM'}}{{{r^2}}}$
Centripetal force on a body of mass $m$ with velocity $v$ and radius of circular path $r$ is written as,
${F_C} = \dfrac{{m{v^2}}}{r}$

Complete step by step answer:
According to the question, we have given the mass density of sphere as,
\rho = \left\\{ {\rho _0},r \leqslant R \\\ \,\,\,\,\,\,\,\,\,\,\,0,r > R \right\\}
So, we see that at distances $r > R$ mass density is zero so, there is no influence of gravitational field hence, the velocity of test mass will be constant after distance $r > R$.

Now, for distances $r < R$ mass density is ${\rho _0}$ Let M, be the test mass and M’ be the mass of sphere and R be the radius of circular path and V be the velocity of test mass then,
to be in circular motion, gravitational force of attraction between test mass and sphere is equal to centripetal force so, using formulas we get
$G\dfrac{{MM'}}{{{r^2}}} = \dfrac{{M{V^2}}}{r}$
$\Rightarrow {V^2} = \dfrac{{GM'}}{r}$

Now, mass of sphere can be written as product of mass density and volume of sphere so,
$M' = {\rho _0}.\dfrac{{4\pi {r^3}}}{3}$ putting this value we get,
$\Rightarrow {V^2} = \dfrac{{G{\rho _0}.\dfrac{{4\pi {r^3}}}{3}}}{r}$
$\Rightarrow {V^2} = G{\rho _0}{r^2}$
So, on taking square root, we get
$V \propto r$
Hence for the distances $r \leqslant R$ velocity is directly proportional to the distance so, the graph will be a straight line having positive slope and for distances $r > R$ velocity will no longer be affected by zero gravitational field so, it will be constant.

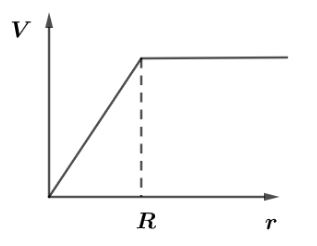
Hence, the correct option is A.

Note: It should be remembered that, here the centripetal force acting on test mass is only due to balancing of gravitational force of attraction between sphere and test mass which gives rise to velocity dependence on distance whereas when there is no gravitational field the velocity of test mass became constant.