Question

A spherical refractive surface of radius 10 cm separates two media of refractive indices µ = 1 and µ = $\frac{3}{2}$ respectively. A point object P starts from rest at t = 0 with an acceleration 2 cm/s². Find the speed of image at t = 1s.

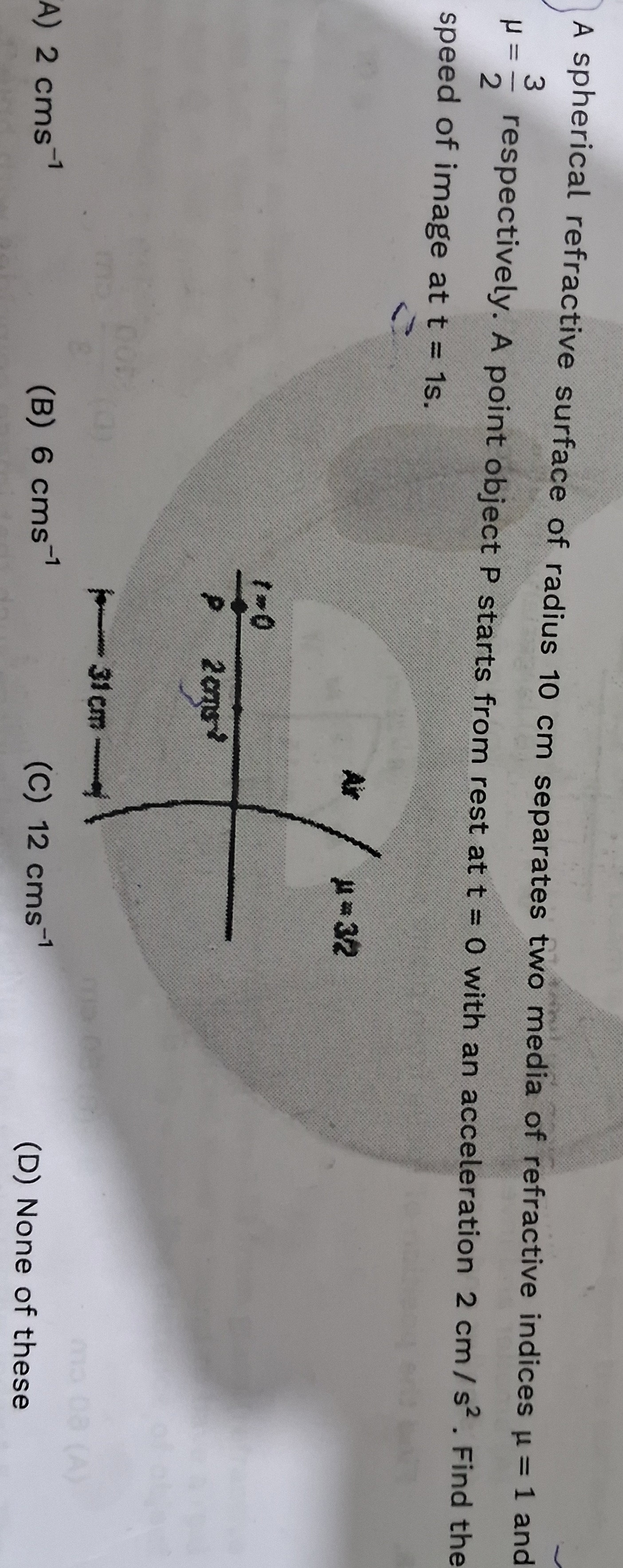
• A. 2 cms⁻¹
• B. 6 cms⁻¹
• C. 12 cms⁻¹
• D. None of these

Answer 1

Answer: (D)

None of these

Answer 2

1. Determine the object's position and velocity at $t = 1$ s: The object starts from rest ($v_0 = 0$) at $t=0$ with an acceleration $a = 2$ cm/s$^2$. Assuming the surface is at the origin and light travels from left to right, and the object is initially 2 cm from the surface, its initial position is $u(0) = -2$ cm. The acceleration is away from the surface, so it's in the negative direction, $a = -2$ cm/s$^2$. The position of the object at time $t$ is given by: $u(t) = u(0) + v_0 t + \frac{1}{2} a t^2$ $u(t) = -2 + (0)t + \frac{1}{2}(-2)t^2 = -2 - t^2$ At $t = 1$ s, the object's position is: $u(1) = -2 - (1)^2 = -3$ cm. The velocity of the object at time $t$ is: $v_{object}(t) = v_0 + at = 0 + (-2)t = -2t$ At $t = 1$ s, the object's velocity is: $v_{object}(1) = -2(1) = -2$ cm/s.

2. Calculate the image position at $t = 1$ s: Using the spherical refractive surface formula: $\frac{\mu_2}{v} - \frac{\mu_1}{u} = \frac{\mu_2 - \mu_1}{R}$ Given: $\mu_1 = 1$, $\mu_2 = 3/2$, $R = +10$ cm, and $u = -3$ cm. $\frac{3/2}{v} - \frac{1}{-3} = \frac{3/2 - 1}{10}$ $\frac{3}{2v} + \frac{1}{3} = \frac{1/2}{10} = \frac{1}{20}$ $\frac{3}{2v} = \frac{1}{20} - \frac{1}{3} = \frac{3 - 20}{60} = -\frac{17}{60}$ $v = \frac{3}{2} \times \left(-\frac{60}{17}\right) = -\frac{90}{17}$ cm.

3. Calculate the image velocity at $t = 1$ s: Differentiate the refractive surface formula with respect to time $t$: $\mu_2 \frac{d}{dt}\left(\frac{1}{v}\right) - \mu_1 \frac{d}{dt}\left(\frac{1}{u}\right) = 0$ $-\frac{\mu_2}{v^2} \frac{dv}{dt} + \frac{\mu_1}{u^2} \frac{du}{dt} = 0$ Let $v_{image} = \frac{dv}{dt}$ and $v_{object} = \frac{du}{dt}$. $-\frac{\mu_2}{v^2} v_{image} + \frac{\mu_1}{u^2} v_{object} = 0$ $v_{image} = \frac{\mu_1}{\mu_2} \frac{v^2}{u^2} v_{object}$ Substitute the values at $t=1$ s: $u = -3$ cm, $v = -90/17$ cm, $v_{object} = -2$ cm/s, $\mu_1 = 1$, $\mu_2 = 3/2$. $v_{image} = \frac{1}{3/2} \frac{(-90/17)^2}{(-3)^2} (-2)$ $v_{image} = \frac{2}{3} \frac{(90/17)^2}{9} (-2)$ $v_{image} = \frac{2}{3} \frac{8100/289}{9} (-2)$ $v_{image} = \frac{2}{3} \frac{900}{289} (-2) = -\frac{1200}{289}$ cm/s.

4. Find the speed of the image: The speed of the image is the magnitude of its velocity: Speed $= |v_{image}| = \left|-\frac{1200}{289}\right| = \frac{1200}{289}$ cm/s. Calculating the numerical value: $\frac{1200}{289} \approx 4.152$ cm/s.

   Since this value is not among the options A, B, or C, the correct option is (D) None of these.