Question

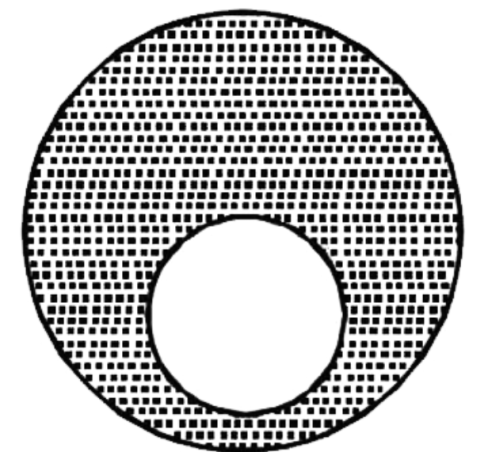
A spherical portion has been removed from a solid sphere having a charge distributed
uniformly in its volume as shown in the figure. The electric field inside the emptied
space is :
(A) zero everywhere
(B) non-zero and uniform
(C) non- uniform
(D) zero at only its centre

Answer 1

Gauss Law states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.

Complete step by step answer:
According to the Gauss law, the total flux linked with a closed surface is $\dfrac{1}{{{\varepsilon _o}}}$ times the charge enclosed by the closed surface,
$\oint {\overrightarrow E .\overrightarrow {ds} = \dfrac{q}{{{\varepsilon _o}}}}$
The electric flux from any closed surface is only due to the sources (positive charges) and sinks (negative charges) of electric fields enclosed by the surface. Any charges outside the surface do not contribute to the electric flux. Also, only electric charges can act as sources or sinks of electric fields. Changing magnetic fields, for example, cannot act as sources or sinks of electric fields.
If a Gaussian surface is constructed within the cavity then by Gauss Law,
$\oint {\overrightarrow E .\overrightarrow {ds} = 0}$
But this does not mean that $\overrightarrow E = 0$
From the figure given in the question, consider a point P inside the cavity and let $\rho$ be the charge density. Then, after applying superposition principle the net electric field at point P will be:
$\overrightarrow E = \dfrac{\rho }{{3{\varepsilon _o}}}\overrightarrow b - \dfrac{\rho }{{3{\varepsilon _o}}}\overrightarrow a$
$\overrightarrow E = \dfrac{\rho }{{3{\varepsilon _o}}}\overrightarrow r$ (Since $\overrightarrow r = \overrightarrow b - \overrightarrow a$)
which for a given cavity is independent of the position of a point within the cavity.
Therefore, we come to the conclusion that the electric field is non-zero and uniform within the cavity.
So, the final answer is (B) non-zero and uniform.

Note: This question is from the concept of solid sphere but if a hollow sphere is given, then, according to Gaussian's law the electric field inside a charged hollow sphere is zero. This is because the charges reside on the surface of a charged sphere and not inside it and thus the charge enclosed by the gaussian surface is Zero and hence the electric field is also zero.