Question

A spherical of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r), is pressure at r (r < R), then the correct option(s) are:
A. P (r = 0) = 0
B. $\dfrac{P(r=3R/4)}{P(r=2R/3)}=\dfrac{63}{80}$
C. $\dfrac{P(r=3R/5)}{P(r=2R/5)}=\dfrac{16}{21}$
D. $\dfrac{P(r=R/2)}{P(r=R/3)}=\dfrac{20}{27}$

Answer 1

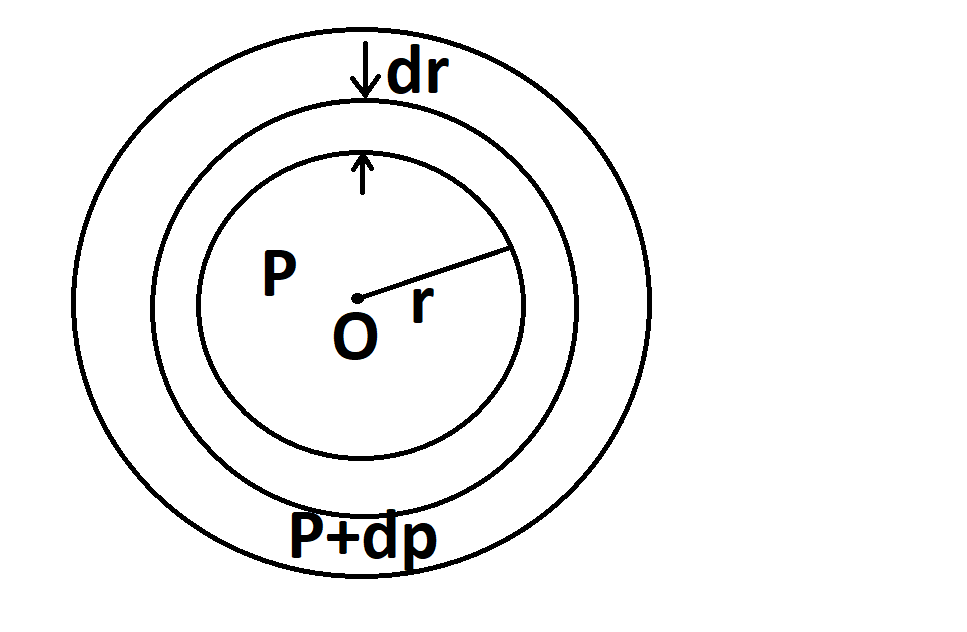
Let g be the acceleration at the direction of the element at distance r from the centre O due to gravity. The difference in pressure (dp) on the two sides of the part in equilibrium is pressure by gravity per unit area.

Complete step by step answer:
So, we have
$-dp=\rho gdr$

Now,
Let the mass of the spherical body with radius r be m
So, now
We have
$m=\dfrac{4}{3}\pi {{r}^{2}}\rho$
Also,
$\Rightarrow g=\dfrac{Gm}{{{r}^{2}}}$
$\Rightarrow g=\dfrac{G}{{{r}^{2}}}\times \dfrac{4}{3}\pi {{r}^{3}}\rho$
$\Rightarrow g=\dfrac{4}{3}G\pi r\rho$
By using the above values,
$dp=-\rho (\dfrac{4}{3}\pi G\rho r)dr$
Integrating both side from P(=R) to P(=r)
We have
$\Rightarrow \int\limits_{P(=R)}^{P(=r)}{dp}=\int\limits_{P(=R)}^{P(=r)}{\rho (-\dfrac{4}{3}G\pi \rho r)}dr$
$\Rightarrow \int\limits_{P(=R)}^{P(=r)}{dp}=-\dfrac{4}{3}G\pi {{\rho }^{2}}\int\limits_{P(=R)}^{P(=r)}{r}dr$
$\Rightarrow \int\limits_{P(=R)}^{P(=r)}{dp}=-\dfrac{4}{3}G\pi {{\rho }^{2}}[\dfrac{{{r}^{2}}}{2}]_{R}^{r}$
$\Rightarrow \int\limits_{P(=R)}^{P(=r)}{dp}=\dfrac{4}{3}G\pi {{\rho }^{2}}[\dfrac{{{R}^{2}}-{{r}^{2}}}{2}]$
$\Rightarrow P(r)-P(R)=\dfrac{4}{3}G\pi {{\rho }^{2}}[\dfrac{{{R}^{2}}-{{r}^{2}}}{2}]$
For,
P(R) = 0, we have P(r) = $\dfrac{4}{3}G\pi {{\rho }^{2}}[\dfrac{{{R}^{2}}-{{r}^{2}}}{2}]$
Now,
When r = 0, P(r) = $\dfrac{4}{3}G\pi {{\rho }^{2}}[\dfrac{{{R}^{2}}}{2}]$
For, $P(r=3R/4)andP(r=2R/3)$
We have
$\dfrac{P(r=3R/4)}{P(r=2R/3)}=\dfrac{63}{80}$
Also, $P(r=3R/5)$ and $P(r=2R/5)$
We have
$\dfrac{P(r=3R/5)}{P(r=2R/5)}=\dfrac{16}{21}$
Now again
For,
$P(r=R/2)$and $P(r=R/3)$
$\dfrac{P(r=R/2)}{P(r=R/3)}=\dfrac{27}{32}$
Therefore, Option – B and Option – C are the correct relations, i.e.,
B. $\dfrac{P(r=3R/4)}{P(r=2R/3)}=\dfrac{63}{80}$
C. $\dfrac{P(r=3R/5)}{P(r=2R/5)}=\dfrac{16}{21}$

Note: In many instances, one may misunderstand the formula of buoyancy for the formula of pressure. Keep in mind that the formula for pressure uses height, whereas, the one for buoyancy uses volume.