Question

A spherical conducting shell of radius R has a charge q. A point charge Q is placed
at its centre. The electrostatic potential at a point P a distance $\dfrac{{\text{R}}}{2}$ from
the centre of the shell is:
A. $\dfrac{{\left( {q + Q} \right)}}{{4\pi {\varepsilon _0}}}\dfrac{2}{R}$
B. $\dfrac{{2Q}}{{4\pi {\varepsilon _0}R}}$
C. $\dfrac{{2Q}}{{4\pi {\varepsilon _0}R}} - \dfrac{q}{{4\pi {\varepsilon _0}R}}$
D. $\dfrac{{2Q}}{{4\pi {\varepsilon _0}R}} + \dfrac{q}{{4\pi {\varepsilon _0}R}}$

Answer 1

The potential at point P at a distance r from the point charge inversely proportional to the distance between the point P and charge q. The potential inside the charged conducting shell remains the same at every point. The potential at point P will be the contribution of potential due to charge placed at the centre of the sphere and the charge distribution on the outer conducting shell.
Formula used:
The potential due to point charge at a distance r is,
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{r}$
Here, ${\varepsilon _0}$ is the permittivity of the free space and Q is the charge.

Complete step by step answer:
Let’s draw the situation given in the question as shown in the figure below.

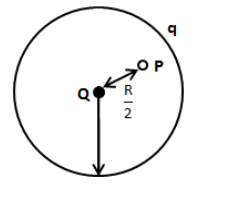
We have the expression for the potential due to point charge at a distance r from the charge
is,
${V_1} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{Q}{r}$
We have given that the position of point P is $\dfrac{{\text{R}}}{2}$ from the centre of the
shell. Therefore, substituting $\dfrac{{\text{R}}}{2}$ for r in the above equation, we get,
${V_1} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2Q}}{R}$……. (1)
We have the expression for the potential inside the charged conducting shell of radius R is,
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{R}$
Here, q is the charge on the sphere.
This potential remains the same at every point inside the sphere. Therefore, the potential at
point P inside the sphere due to charge on the sphere is,
${V_2} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{R}$ ……(2)
Thus, the potential at point P will the sum of the potential due to point charge Q and
potential inside the charged sphere. Therefore, we can write,
$V = {V_1} + {V_2}$

_0}R}}$$ **So, the correct answer is option (D).** **Note:** The potential due to uniform charge distribution of the shell at the point outside the shell is zero. The potential inside the hollow charged conducting shell remains the same at every point due to uniform charge distribution over the surface of the shell. The electric field inside such a shell becomes zero.