Question
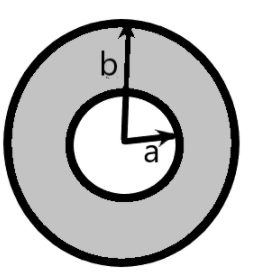
Question: A spherical capacitor has an outer radius of ‘b’ and inner radius ‘a’ with the air as the dielectric...
A spherical capacitor has an outer radius of ‘b’ and inner radius ‘a’ with the air as the dielectric medium. If the ‘a’ is kept constant and the outer radius ‘b’ is increased, what happens to the capacitance?
A) Increases
B) Decreases
C) May increase or decrease
D) None of these.
Solution
We need to find the relation between the outer and inner radii of the spherical capacitor to its capacitance. We are to assume that the spherical capacitor is not connected to an external source. Using these we can find the change in capacitance.
Complete answer:
We are to find the capacitance of a spherical capacitor for understanding the relations between the inner radius and the outer radius of the capacitor in which the dielectric medium is kept.
The capacitance for any shape can be expressed as –
C=dε0A
The area of the spherical shell is given as –
A=4πab
The distance between the plates can be given as –
d=b−a
We can substitute these values in the formula of capacitance to get the capacitance of a spherical capacitor. The capacitance can be given as –