Solveeit Logo
Login

Question

Question: A spherical capacitor has an inner sphere of radius \(12cm\) and an outer sphere of radius \(13cm\)....

A spherical capacitor has an inner sphere of radius 12cm12cm and an outer sphere of radius 13cm13cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5μC2.5\mu C. The space between the concentric spheres is filled with liquid of dielectric constant 32.32.
A) Determine the capacitance of the capacitor.
B) What is the potential of the inner sphere?
C) Compare the capacitance of the capacitor with that of an isolated sphere of radius 12cm12cm. Explain why the latter is much smaller.

Explanation

Solution

The capacitance of a system only depends on the geometry and the medium between the two plates/surfaces. An isolated sphere is nothing but a sphere with one spherical surface(outer one) is taken to infinity.

Formula Used:
Capacitance for spherical capacitor
C=4πε0KrRR−rC=4\pi {{\varepsilon }_{0}}K\dfrac{rR}{R-r}

Complete step by step answer:
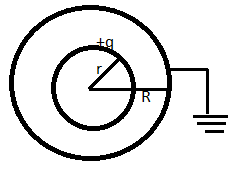
A spherical capacitor consists of a solid or hollow spherical conductor of radius rr, surrounded by another hollow concentric spherical of radius RR.
Potential difference between two conductors
V=q4πε0K(R−r)RrV=\dfrac{q}{4\pi {{\varepsilon }_{0}}K}\dfrac{\left( R-r \right)}{Rr} ………….(i)

Capacitance of spherical conductor
C=qVC=\dfrac{q}{V}
C=qq4πε0K(R−r)Rr=4πε0KRr(R−r)C=\dfrac{q}{\dfrac{q}{4\pi {{\varepsilon }_{0}}K}\dfrac{\left( R-r \right)}{Rr}}=4\pi {{\varepsilon }_{0}}K\dfrac{Rr}{\left( R-r \right)}
(a) C=4πε0K(R−r)RrC=4\pi {{\varepsilon }_{0}}K\dfrac{\left( R-r \right)}{Rr} ………………….(ii)
Where
R=R= Outer sphere radius
r=r= Inner sphere radius
K=K= Dielectric constant
K=32K=32
R=13cm=13×10−2mR=13cm=13\times {{10}^{-2}}m
r=12cm=12×10−2mr=12cm=12\times {{10}^{-2}}m
C=19×10932×13×10−2×12×10−2(13−12)×10−2C=\dfrac{1}{9\times {{10}^{9}}}\dfrac{32\times 13\times {{10}^{-2}}\times 12\times {{10}^{-2}}}{\left( 13-12 \right)\times {{10}^{-2}}}
C=554.66×10−11C=554.66\times {{10}^{-11}}
C=5.5×10−9FC=5.5\times {{10}^{-9}}F
(b)
V=qC ⇒V=2.5×10−65.5×10−9 ⇒V=4.5×102 ⇒V=450V \begin{aligned} & V=\dfrac{q}{C} \\\ & \Rightarrow V=\dfrac{2.5\times {{10}^{-6}}}{5.5\times {{10}^{-9}}} \\\ & \Rightarrow V=4.5\times {{10}^{2}} \\\ & \Rightarrow V=450V \\\ \end{aligned}
(c)For isolated sphere
R→∞R\to \infty
C=4πε01(1r−1R) C′=4πε0r \begin{aligned} & C=4\pi {{\varepsilon }_{0}}\dfrac{1}{\left( \dfrac{1}{r}-\dfrac{1}{R} \right)} \\\ & C'=4\pi {{\varepsilon }_{0}}r \\\ \end{aligned}
⇒C′=19×109×12×10−2 ⇒C′=1.33×10−11F \begin{aligned} & \Rightarrow C'=\dfrac{1}{9\times {{10}^{9}}}\times 12\times {{10}^{-2}} \\\ & \Rightarrow C'=1.33\times {{10}^{-11}}F \\\ \end{aligned}

The capacity of an isolated sphere is much smaller, because in a capacitor, the outer sphere is earthed, potential difference decreases and capacitance increases.

Note: When we find out the capacitance for hollow spherical capacitors sometimes we use the formula of a single sphere capacitor directly. This is the wrong method first we find out the potential difference between the spheres and then capacitance.