Question
Question: A spherical bob of mass m and charge q suspended from a string of length l rotates about a fixed cha...
A spherical bob of mass m and charge q suspended from a string of length l rotates about a fixed charge identical to that of the bob (Fig.). The angle between the string and the vertical is q. Find the angular velocity of uniform rotation of the bob. It is given that ml2kq2=g
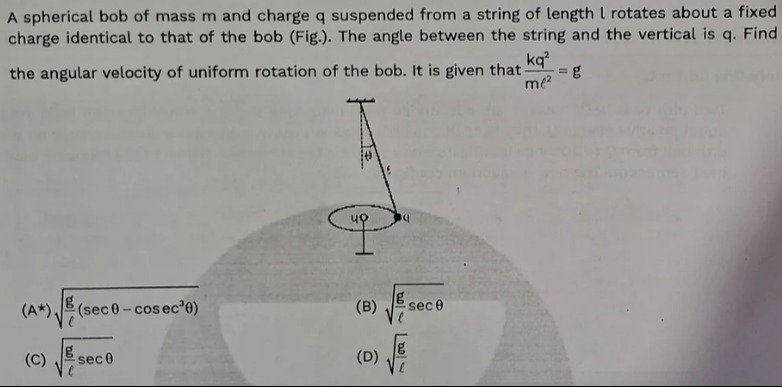
lg(secθ−cosec3θ)
lgsecθ
lgsecθ
lg
lg(secθ−cosec3θ)
Solution
To find the angular velocity of the bob, we analyze the forces acting on it: tension in the string, weight, and electrostatic force.
-
Vertical Equilibrium: The vertical component of tension balances the weight:
Tcosθ=mg⟹T=cosθmg -
Horizontal Force Balance: The horizontal component of tension and the electrostatic force provide the centripetal force:
Tsinθ−Fe=mω2(lsinθ) -
Electrostatic Force: Given Fe=(lsinθ)2kq2 and ml2kq2=g, we get:
Fe=sin2θmg -
Substitute and Solve: Substituting T and Fe into the horizontal force balance equation:
mgtanθ−sin2θmg=mω2lsinθDividing by mlsinθ:
ω2=lsinθg(tanθ−sin2θ1) -
Simplify: Expressing in terms of secθ and cscθ:
ω2=lg(secθ−csc3θ)Thus,
ω=lg(secθ−csc3θ)
