Question

A spherical balloon of radius r subtends an angle $\alpha$ at the eye of an observer, while the angle of elevation of its center is $\beta$. The height of the center of the balloon is
(a) $r\cos \left( \dfrac{\beta }{2} \right)\sin \alpha$
(b) $r\csc \beta \sin \left( \dfrac{\alpha }{2} \right)$
(c) $r\csc \left( \dfrac{\alpha }{2} \right)\sin \beta$
(d) $r\csc \left( \dfrac{\alpha }{2} \right)\sin \left( \dfrac{\beta }{2} \right)$

Answer 1

Hint: Draw the figure as per the question. Take O as the center of balloon and P as the observer. Draw tangent PA and PB to the circle from P. To find height, draw a line from center to ground. Thus consider the triangles formed, using sine function to find the height.

Complete step-by-step answer:

Given to us a spherical balloon of radius r. Let us take the center of the spherical balloon as O. Let the point P be the eye of an observer, as shown in the figure.

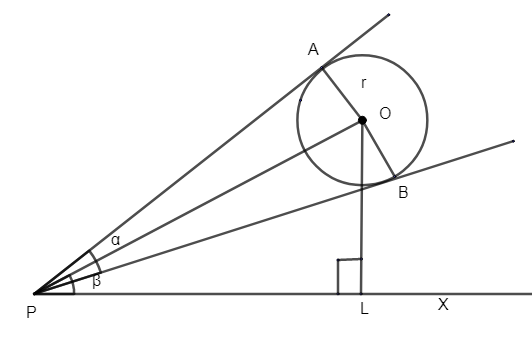
Let PA and PB be the tangents from point P to the balloon.
From the figure, we can say that, $\angle APB=\alpha$.
Angle $\alpha$, bisects such that, $\angle APO=\angle BPO=\dfrac{\alpha }{2}$.
Let OL be the height of the balloon drawn from the center O to the ground.
From the figure we can say that, $\angle OPL=\beta$.
Now, let us consider $\Delta OPL$, which is right angled at L as, $OL\bot PX$.
$\therefore$ From $\Delta OPL$,
$\sin \beta$ = opposite side / hypotenuse = $\dfrac{OL}{OP}$.
$\therefore \sin \beta =\dfrac{OL}{OP}\Rightarrow OL=OP\sin \beta -(1)$
Now let us consider, $\Delta OAP$, right angle at A i.e. $AO\bot PO$.
[Because a line tangent to a circle is perpendicular to the radius drawn to the point of tangency]
$\sin \dfrac{\alpha }{2}$ = opposite side / hypotenuse
$\sin \dfrac{\alpha }{2}=\dfrac{OA}{OP}$
We know that, OA = r.
$\therefore \sin \dfrac{\alpha }{2}=\dfrac{r}{OP}\Rightarrow OP=\dfrac{r}{\sin \dfrac{\alpha }{2}}=r\csc \dfrac{\alpha }{2}$
We know that, $\csc \theta =\dfrac{1}{\sin \theta }$, which is a basic trigonometric function.
$\therefore OP=r\csc \dfrac{\alpha }{2}-(2)$
Let us put (2) in (1).
$OL=OP\sin \beta =r\csc \dfrac{\alpha }{2}.\sin \beta$
We said that OL is the height of the center of the balloon.
Thus, height = $r\csc \left( \dfrac{\alpha }{2} \right).\sin \beta$.
$\therefore$ Option (c) is the correct answer.

Note: It is difficult to draw the figure, if you don’t understand the concept of the question. You might get confused about how $\alpha$ and $\beta$ are formed in the figure. Thus remember the steps we have done and understand the figure thoroughly.And also Students should remember trigonometric formulas, ratios and identities to solve these types of questions.