Question
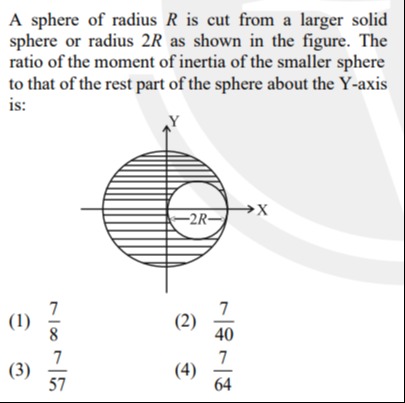
Question: A sphere of radius $R$ is cut from a larger solid sphere or radius $2R$ as shown in the figure. The ...
A sphere of radius R is cut from a larger solid sphere or radius 2R as shown in the figure. The ratio of the moment of inertia of the smaller sphere to that of the rest part of the sphere about the Y-axis is:
87
407
577
647
577
Solution
Let Rlarge=2R be the radius of the larger sphere and Rsmall=R be the radius of the smaller sphere. Let ρ be the density of the solid sphere.
The mass of the larger sphere is Mlarge=ρ⋅34πRlarge3=ρ⋅34π(2R)3=ρ⋅332πR3. The mass of the smaller sphere is msmall=ρ⋅34πRsmall3=ρ⋅34πR3.
The larger sphere is centered at the origin. The Y-axis passes through the center of the larger sphere. The moment of inertia of the larger solid sphere about the Y-axis is Ilarge=52MlargeRlarge2=52(ρ332πR3)(2R)2=52(ρ332πR3)(4R2)=15256πρR5.
From the figure, we assume the smaller sphere is centered at a distance of R from the origin along the X-axis. So, the center of the smaller sphere is at (R,0,0). The Y-axis is the axis of rotation. The distance from the center of the smaller sphere to the Y-axis is d=R.
The moment of inertia of the smaller sphere about an axis passing through its center and parallel to the Y-axis is Ismall,center=52msmallRsmall2=52(ρ34πR3)R2=158πρR5. Using the parallel axis theorem, the moment of inertia of the smaller sphere about the Y-axis is Ismall=Ismall,center+msmalld2=52msmallR2+msmall(R)2=57msmallR2. Substituting the value of msmall: Ismall=57(ρ34πR3)R2=1528πρR5.
The rest part of the sphere is the larger sphere with the smaller sphere removed. By the principle of superposition, the moment of inertia of the rest part about the Y-axis is the moment of inertia of the larger sphere minus the moment of inertia of the smaller sphere about the Y-axis. Irest=Ilarge−Ismall=15256πρR5−1528πρR5=15228πρR5.
The ratio of the moment of inertia of the smaller sphere to that of the rest part of the sphere about the Y-axis is: Ratio = IrestIsmall=15228πρR51528πρR5=22828=577.
Therefore, the ratio is 577.
