Question

A sphere of radius 4cm is given a charge of $16\mu C$. If the sphere is situated in air then the electric field at a point at a distance of 2cm from the centre of the sphere is:

A. $36 \times {10^7}N{C^{ - 1}}$
B. $9 \times {10^7}N{C^{ - 1}}$
C. 0
D. $4 \times {10^7}N{C^{ - 1}}$

Answer 1

To solve this question we first need to know about the electric field through gauss law. We will first define gauss law and then relate it to the question. We will know about the electric fields inside the sphere within the radius.

Formula Used;
$\vec E = \dfrac{1}{{{\varepsilon _0}}}q$
Where,
$\vec E$= electric field
$q$= charge enclosed in a Gaussian surface.

Complete step by step solution:
Let us look at gauss law first:
Gauss law: it states that the electric field inside a Gaussian surface is $\dfrac{1}{{{\varepsilon _0}}}$the total charge enclosed in it.
Let us now consider a sphere of radius 4cm.

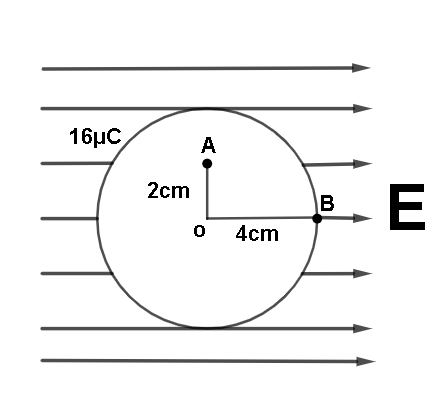
This sphere will be considered as the Gaussian surface. The Gaussian surface is placed inside an electric field . Here the electric field is constant. Outside the surface of this sphere the electric field is given by $E = \dfrac{1}{{4\pi {\varepsilon _0}}}q$. In this case the whole charge is supposed to be on the surface of the sphere( it means the $16\mu C$charge is equally distributed on the surface) To find an electric field at 2cm (2cm<4cm) it means we have to find an electric field inside the hollow sphere. Inside the sphere the electric field will be 0 as all the charge is distributed on the surface of the sphere .
Hence the correct answer to this question is option C.

Note: looking at the question you might think that it can be solved just using the formula for electric field $E = \dfrac{1}{{4\pi {\varepsilon _0}}}q$ because charge and radius has been given. But that would be wrong because to consider an electric field we need to consider the charge on the Gaussian surface only and not anywhere else except it.