Question
Question: A sphere of mass \(m\) is given some angular velocity about a horizontal axis through its centre and...
A sphere of mass m is given some angular velocity about a horizontal axis through its centre and gently placed on the plank of mass m. The coefficient of friction between the two is μ. The plank rests on a smooth horizontal surface. The initial acceleration of centre of mass of the sphere relative to the plank will be:
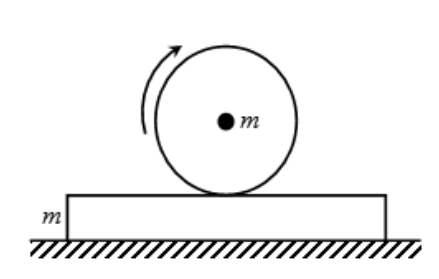
Solution
To solve this problem we need to use the formula of the rotational equivalent of Newton’s second law of motion. From that, we need to find the angular velocity from the previous equation. And then we need to find the individual acceleration of both the sphere and plank using the rearranged form of Newton’s second law. The next step is to find the relative acceleration of the sphere with respect to plank.
Complete step by step answer:
The analogous equation to Newton’s second law of motion that involves torque and rotational motion we get,
F=mr×α ……. (1)
Here m is the mass of the body and r is the radius of the body, α is said to be the angular velocity of the rotating object and F is the force.
Multiplying both sides by r in the above equation we get,
F×r=mr2×α …….. (2)
Since in the question we have a frictional force we can write equation (2) we get,
Ffric×r=mr2×α ……. (3)
Let μbe the coefficient of friction. Therefore the frictional force can be written as,
Ffric=Nμ
Where N is the normal force and also N=mg. The above equation becomes,
Ffric=mgμ …… (4)
Substituting equation (4) in equation (3)
mgμ×r=mr2×α
Rearranging the above equation we get,
α=mr2mgμ×r
⇒α=Imgμ×r.....(Since I=mr2)
There are some standard values of moment of inertia for different shapes. In that the moment of inertia of the sphere is given by,
I=mr2=52mr2
⇒α=52mr2mgμ×r ……. (5)
⇒α=25rμg ……. (6)
Now the initial acceleration of sphere and plank can be found by,
The initial acceleration of the sphere can be found using equation (2),
F×r=mr2×α
Here we can substitute for force as F=ma
ma×r=mr2×α
If we rearrange this equation to get acceleration we get,
asphere=rα
⇒asphere=r×25rμg......(From equation 6)
⇒asphere=25μg
The initial acceleration of the plank can be found by,
a=mF
Since force in the plank includes the frictional force in the opposite direction we have,
aplank=mμmg (SinceFfric=NμandN=mg)
Also while calculating the acceleration of the plank we also need to take into account the mass of the sphere. Therefore adding its mass to the above equation we get,
aplank=m+mμmg
⇒aplank=2mμmg
⇒aplank=2μg
Now the initial acceleration of the centre of mass of the sphere relative to the plank is
arel=asphere−aplank
⇒arel=25μg−(2μg)
⇒arel=24μg
∴arel=2μg m/s2
Therefore acceleration of centre of mass of the sphere with relative to the plank will be 2\mu g$$$$m/{s^2}.
Note: The centre of mass is the point in a system or body in which the whole mass of the particular object will be focused or concentrated. We can consider the whole mass of the body on that particular point which is called the centre of mass. The idea of the centre of mass (COM) is essential in examining the movement of the system of objects.
