Question

A sphere of mass 4 kg is at rest as shown with help of a horizontal rod of mass 2 kg. Friction between rod & sphere and between sphere & plane is sufficient. One end of the rod is hinged with plane.

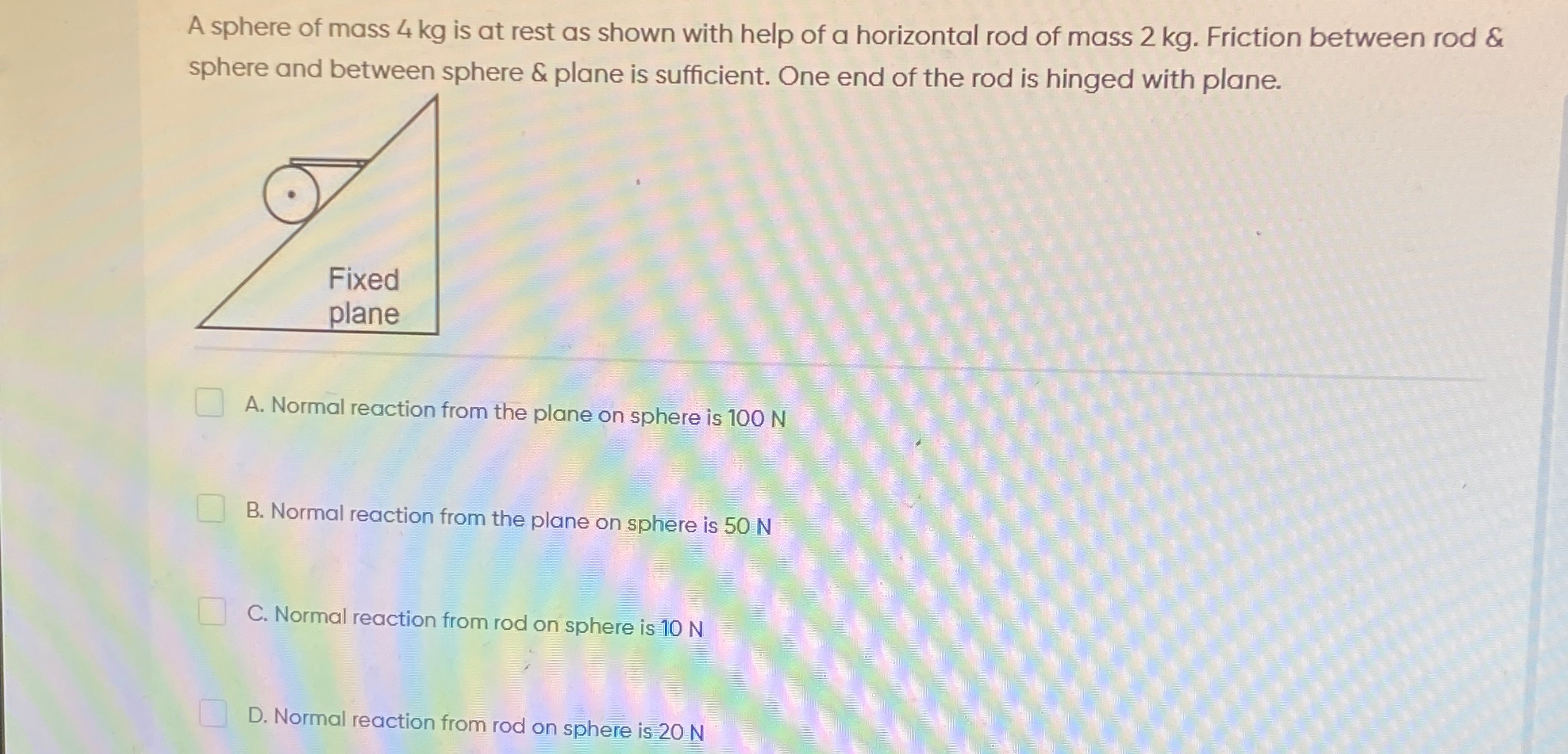
• A. Normal reaction from the plane on sphere is 100 N
• B. Normal reaction from the plane on sphere is 50 N
• C. Normal reaction from rod on sphere is 10 N
• D. Normal reaction from rod on sphere is 20 N

Answer 1

Answer: (B), (C)

Option B (50 N from plane on sphere) and Option C (10 N from rod on sphere).

Answer 2

We shall show that using g = 10 m/s² the forces “working” on the sphere add up as follows. (Our treatment ignores the friction‐limits since it is only assumed “sufficient” to hold equilibrium.)

1. The 4‐kg sphere weighs 4g = 40 N. It is not self‐supported on the (inclined) plane because a horizontal rod is used to “assist” its support.

2. The rod (of 2 kg, weight 2g = 20 N) is hinged at one end. Writing moment–equilibrium about the hinge we see that its own weight (acting at mid‐length, a lever arm L/2) is balanced by the force due to the sphere acting at the other end (lever arm L). Thus the force (that is, the normal reaction at the contact) is

   R = (20 N × (L/2))/L = 10 N.

   But by Newton’s third law the rod pushes on the sphere with 10 N.

3. Now the sphere is acted on by its 40 N weight and also by the 10 N from the rod (which, because the rod is horizontal and touches the sphere’s top, acts vertically downward on the sphere). Thus the total vertical load transmitted to the plane is

   40 N + 10 N = 50 N.

   So the reaction from the plane on the sphere must be 50 N.

Thus the normal reaction from the plane on the sphere is 50 N and the normal reaction from the rod on the sphere is 10 N.