Question

A sphere of diameter r is cut from a solid sphere of radius r such that the centre of mass of remaining part be at maximum distance from original centre, then this distance is:

Answer 1

Calculate the mass of sphere cut from the whole sphere using the relation between density, volume and mass. To calculate the mass of the remaining sphere, subtract the mass of the small sphere from the original mass of the sphere. Use the equation of COM to determine the distance.

Formula used:
$COM = \dfrac{{{m_1}{r_1} + {m_2}{r_2} + ...}}{{{m_1} + {m_2} + ..}}$, where, m is the mass and r is the distance between origin and mass m.

Complete step by step answer:
We have given, the centre of mass of the remaining part is at maximum distance from the original centre of the sphere after we cut the small sphere of radius $\dfrac{r}{2}$ from it. Therefore, we can draw the figure as below,

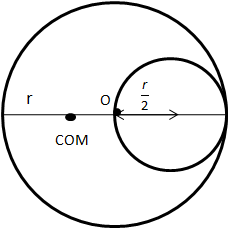
Let the distance between position of centre of mass and original centre of the sphere.
The mass of the sphere before the small sphere is cut from it is,
$M = \dfrac{4}{3}\pi {r^3}\rho$
The mass of the small sphere of radius $\dfrac{r}{2}$ is,
$m = \dfrac{4}{3}\pi {\left( {\dfrac{r}{2}} \right)^3}\rho$
$\Rightarrow m = \dfrac{1}{8}\left( {\dfrac{4}{3}\pi {r^3}\rho } \right)$ …… (1)
The mass of the remaining sphere is now,
$M' = M - m$
$\Rightarrow M' = \left( {\dfrac{4}{3}\pi {r^3}\rho } \right) - \dfrac{1}{8}\left( {\dfrac{4}{3}\pi {r^3}\rho } \right)$
$\Rightarrow M' = \dfrac{7}{6}\pi {r^3}\rho$ …… (2)
The position of the centre of mass of the total sphere is zero. Therefore, we can express the centre of mass of system of two spheres as follows,
$0 = \dfrac{{ - xM' + \dfrac{r}{2}m}}{{M' + m}}$
$\Rightarrow - xM' + \dfrac{r}{2}m = 0$
$\Rightarrow xM' = \dfrac{r}{2}m$
Use equation (1) and (2) to rewrite the above equation as follows,
$\Rightarrow x\left( {\dfrac{7}{6}\pi {r^3}\rho } \right) = \dfrac{r}{2}\left( {\dfrac{1}{8}\left( {\dfrac{4}{3}\pi {r^3}\rho } \right)} \right)$
$\Rightarrow x\left( {\dfrac{7}{6}} \right) = \left( {\dfrac{r}{2}} \right)\left( {\dfrac{1}{6}} \right)$
$\Rightarrow x = \dfrac{r}{{14}}$
Therefore, the position of centre of mass of the remaining sphere from the original centre of the sphere is $\dfrac{r}{{14}}$.

Note:
The centre of mass of the spherical system is zero because the sphere is assumed to have uniform density. Therefore, the centre of mass lies at the centre of the sphere. We have assumed the centre of the sphere as the origin for measurement of distances. Therefore, the distance x is taken as negative.