Question

A sphere is suspended by a thread of length $l$ . What minimum horizontal velocity has to be imparted to the ball for it to reach the height of the suspension?
(A) $gl$
(B) $2gl$
(C) $\sqrt {gl}$
(D) $\sqrt {2gl}$

Answer 1

Hint : Here, a sphere is given and it is suspended by a thread of length $l$ with minimum horizontal velocity is applied to the sphere so that it reaches the height of the suspension that is also $l$ . Here, we have to use the concept of conservation of energy theorem. Draw the suitable diagram and give proper names.

Complete Step By Step Answer:
Here, the length of the thread is $l$ and the sphere is tied to it. The minimum velocity applied to the sphere is $v$ . The diagram shows the representation of the suspension of the sphere.

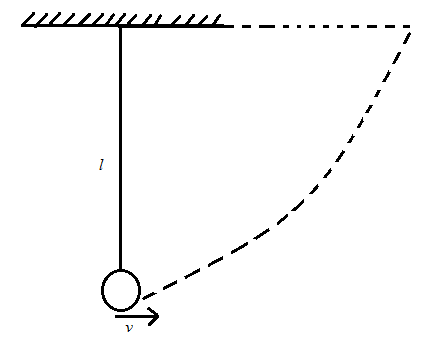
Therefore, let us use the energy conservation formula as given below:
$K.E. = P.E$
Kinetic energy is the energy when the sphere is given the velocity, the sphere stores kinetic energy. When the sphere reaches the height of suspension it stores the potential energy.
Thus the energy is conserved in the initial and final stage.
Kinetic energy is the initial form of energy and potential energy is the final form of energy.
Hence,
$\dfrac{1}{2}m{v^2} = mgl$
$\Rightarrow {v^2} = 2gl$
$\Rightarrow v = \sqrt {2gl}$
The minimum velocity of the sphere at the height of suspension is $\sqrt {2gl}$
The correct answer is the option D.

Note :
Here, the concept we used is the conservation of energy. Kinetic energy depends on the mass and velocity of the object and it is the initial form of energy in this problem and potential energy depends on the mass, length and acceleration due to gravity is the final form of energy.