Question

A sphere is accelerated upwards by a cord whose breaking strength is four times its weight. The maximum acceleration with which the sphere can move up without breaking the cord is:
A. g
B. 3g
C. 2g
D. 4g

Answer 1

The breaking strength of the cord can be used to determine the weight of the sphere, as the force with which the sphere can be accelerated without breaking the cord is proportional to the breaking strength of the cord and vice-versa.

Formula used:
$F=T-W$

Complete answer:
From given, we have the data,
The weight of the sphere is, $W=mg$
The breaking strength of the cord which is used to accelerate the sphere upwards is four times the weight of the sphere, $T=4\times W$
$\therefore T=4mg$

The diagram representing the forces acting on the sphere is,

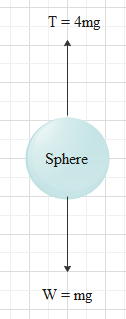
The maximum amount of force should be acting on the sphere in order to have the maximum acceleration with which it can move up without breaking the cord.

Thus, the acceleration is given as,
$F=T-W$ …… (1)
Where $F$ is the maximum force acting on the sphere, $T$ is the breaking strength of the cord and $W$ is the weight of the sphere.
$F=ma$
Where $m$ is the mass of the sphere and $a$is the acceleration of the sphere.

Now substitute the values of $F,\,T\,\And \,W$ in the equation (1).
So, we get,
$ma=4mg-mg$
As the mass is on both sides of the equation, take it as common.
$ma=m(4g-g)$
Upon cancelling out the mass, we get,
$a=3g$
Where $g$ is the gravitational constant.

So, the correct answer is “Option B”.

Note:
The things to be on your figure tips for further information on solving these types of problems are: The weight of the sphere should be subtracted from the breaking strength of the cord carrying the sphere, as both are acting in opposite directions.