Question

A sphere floats in water just submerged as shown in the diagram. If atmospheric pressure is neglected then:-

A) Force exerted by liquid on lower half of sphere is $\dfrac{{4\rho \pi {R^3}}}{3}8$
B) Force exerted by liquid on lower half of sphere and upper half of sphere is same in magnitude
C) Ratio of magnitude of forces exerted by liquid on lower and upper half of sphere is 5:1
D) Ration magnitude of forces exerted by liquid on lower and upper half of sphere is 4:1

Answer 1

In order to solve the question we first check the options, there are only forces and magnitude and their ratios. So we will start calculating the forces at the top and bottom of the sphere and then calculate the ratio between them. And then check the options.

Complete step by step answer:
Step 1:
We are given:
A sphere floats in water just submerged, and if atmospheric pressure is neglected then we have to choose from the above given options.
Any one option will be right.
So let us start to find the forces first which are acting on the liquid.
To understand the forces acting on the sphere inside the water we have a diagram to show:
In the diagram the sphere is just touching the surface of the water and the rest of the part is inside of water. There will be a force acting from outside the water and an upward thrust also be acting at the bottom of the sphere shown in the diagram:
Let ${F_1}$ be the force acting on the upper half of the sphere.
And also let ${F_2}$ be the force acting as an upthrust in the water

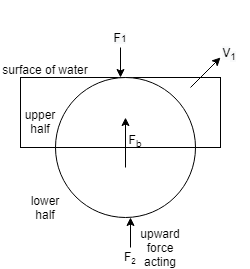
Step 2:
Now coming to the question:
${F_1}$ Is the weight of the water above the top half of the sphere.
Here ${F_1}$ =$V\rho g$ …. (1) where, V is the volume, g is the gravity and $\rho$ is the density of water.
The total volume of the upper half of the sphere in water will be the total volume subtracted by the half volume of the sphere.
The volume of the sphere is $\dfrac{4}{3}\pi {R^3}$ and half of the volume be $\dfrac{2}{3}\pi {R^3}$
Now substituting it to find the V we get, $\pi {R^2} \times R - \dfrac{2}{3}\pi {R^3}$ × $\rho g$
Taking out the common terms outside and putting in (1) then the ${F_1}$will be $\dfrac{{\pi {R^3}}}{3}\rho g$ ……… (2)
Another force ${F_2}$ is acting at the base of the sphere.
Hence ${F_b}$ which is the force of the buoyancy will be equal to ${F_2} - {F_1}$
From here we can find out the force acting at the bottom of the sphere.
So, ${F_2}$=$\dfrac{{\pi {R^3}}}{3}\rho g + \dfrac{4}{3}\pi {R^3} \times \rho g$
Taking out the common terms and solving it further we get ${F_2}$ =$\dfrac{5}{3}\pi {R^3}\rho g$…. (3)
Now we will find out the ratio of both the force acting at the surface and the bottom of the sphere.
Then, $\dfrac{{{F_2}}}{{{F_1}}}$ =$\dfrac{{\dfrac{5}{3}\pi {R^3}\rho g}}{{\dfrac{{\pi {R^3}}}{3}\rho g}}$ is equal to the ratio 5:1
Hence, Ratio of magnitude of forces exerted by liquid on lower and upper half of sphere is 5:1

Option C is the correct answer.

Note: The reason why we have started with the forces acting upward and the downward is that in such questions we need to work according to the option demand. In most of the options we have seen that there is the ratio of the magnitude of forces and hence it has given clues to start with the calculating forces.