Question

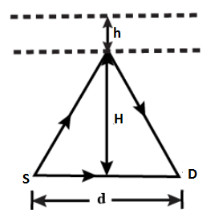
A source $S$ and a detector $D$ of high frequency waves are a distance $d$ apart on the ground. The direct wave from $S$ is found to be in phase at $D$ with the wave from $S$ that is reflected rays making the same angle with the reflecting layer. When the layer rises a distance $h$ , no signal is detected at $D$ . Neglect absorption in the atmosphere and find the relation between $d$ , $h$ , $H$ and the wavelength $\lambda$ of the waves.

Answer 1

Hint : In order to solve this question, we are going to consider the two rays that are approaching the point $D$ first from the height $H$ and then from the height $\left( {H + h} \right)$ . The first one will form constructive interference and the latter will be destructive. Thus, respective path differences are subtracted.
The path difference for constructive interference is given by
$\Delta x = n\lambda$
The path difference for destructive interference is given by
$\Delta x = \left( {n + \dfrac{1}{2}} \right)\lambda$ .

Complete Step By Step Answer:
If we observe the situation as given in the question, we see that when a ray is reflected from a height $H$ , and the other one comes to $D$ in a direct way, then, the interference that occurs is a constructive one.
We know that the path difference for constructive interference is given by
$\Delta x = n\lambda$
Where,
$n = 0,1,2,3,....$
Let us consider a point P at the height $H$
Thus, $SD = d$
$SP = \sqrt {{H^2} + {{\left( {\dfrac{d}{2}} \right)}^2}}$
And, $PD = \sqrt {{H^2} + {{\left( {\dfrac{d}{2}} \right)}^2}}$
Hence, $SP + PD = 2\sqrt {{H^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} = \sqrt {4{H^2} + {d^2}}$
Hence, the path difference is given by
\Delta x = SP - SD = \sqrt {4{H^2} + {d^2}} - d \\\ \Rightarrow n\lambda = \sqrt {4{H^2} + {d^2}} - d - - - - \left( 1 \right) \\\
When ray comes from height $H + h$ , there is no direct ray coming to $D$ , then the destructive interference occurs at $D$
Now, path difference for destructive interference is given by
$\Delta x = \left( {n + \dfrac{1}{2}} \right)\lambda$
Where, $n = 0,1,2,3,....$
Let us consider a point Q at the height $H + h$
$SD = d$
And
SQ = \sqrt {{{\left( {H + h} \right)}^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} \\\ QD = \sqrt {{{\left( {H + h} \right)}^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} \\\
Thus, $SQ + QD = 2\sqrt {{{\left( {H + h} \right)}^2} + {{\left( {\dfrac{d}{2}} \right)}^2}} = \sqrt {4{{\left( {H + h} \right)}^2} + {d^2}}$
Hence, the path difference is given by
SQ - SD = \sqrt {4{{\left( {H + h} \right)}^2} + {d^2}} - d \\\ \Rightarrow \left( {n + \dfrac{1}{2}} \right)\lambda = \sqrt {4{{\left( {H + h} \right)}^2} + {d^2}} - d - - - - \left( 2 \right) \\\
Subtracting equation $\left( 1 \right)$ from equation $\left( 2 \right)$
$\lambda = 2\sqrt {4{{\left( {H + h} \right)}^2} + {d^2}} - 2\sqrt {4{H^2} + {d^2}}$

Note :
For both the constructive and the destructive interference, two factors that remain common are the variable $n$ and the wavelength, the respective relations for both the types are different which gives two different equations and thus, helps to solve for the value of the wavelength.