Question

A source of wave produces 1 crest and 1 trough in 16s. Find the frequency of the wave.
A. .0625 Hz
B. 16 Hz
C. 100
D. 0 Hz

Answer 1

Firstly we will compute the time period of the wave by dividing the time by the number of crests or troughs. Then, we will compute the reciprocal of the obtained value of the time period to get the value of the frequency of the wave.
Formulae used:
$f=\dfrac{1}{T}$
$T=\dfrac{t}{n}$

Complete step-by-step solution:
The diagram of a wave.

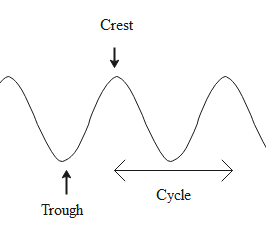
Crest – the highest point or the surface of the wave above the rest position.
Trough – the lowest point or the surface of the wave below the rest position
A crest and a trough make up one cycle or the wavelength of a wave.
From the given information, we have the data as follows.
The time taken by the wave, $t=16\,s$
The number of crests or troughs, $n=1$
The formula that defines the relation between the time period and the frequency of a wave is given as follows.
$f=\dfrac{1}{T}$
Where $f$ is the frequency and $T$ is the time period.
Firstly we will compute the time period of a wave concerning the number of crests and troughs.
The time period of a wave is equal to the number of crests or troughs by the time taken.
Therefore, the time period is,
$T=\dfrac{t}{n}$
Where $t$is the time taken and $n$ is the number of crests or troughs.
Substitute the values in the above formula.

& T=\dfrac{16}{1} \\\ & \Rightarrow T=16\,s \\\ \end{aligned}$$ Therefore, the value of the time period of the wave is $$16s$$. As, the number of crests and troughs produced equals 1, thus, the time taken and the time period values are the same. Now, using this value of the time period of the wave, we will compute the frequency of the wave. Consider the formula $$f=\dfrac{1}{T}$$ Substitute the values in the above formula. $$\begin{aligned} & f=\dfrac{1}{16} \\\ & \Rightarrow f=0.0625\,Hz \\\ \end{aligned}$$ **$$\therefore $$The value of the frequency of the wave is $$0.0625\,Hz$$, thus, the option (A) is correct.** **Note:** The time taken by the wave to produce crests and troughs is different from the time period of the wave. The time period is the time taken by a wave to complete one cycle.