Question

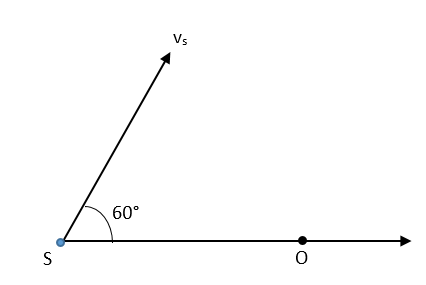
A source of sound 'S' emitting waves of frequency 100 Hz and an observer 'O' are located at some distance from each other. The source is moving with a speed of 19.4 $m{s^{ - 1}}$ at an angle of 60° with the source observer line as shown in the figure. The observer is at rest. The apparent frequency observed by the observer is ? (velocity of sound in air 330 $m{s^{ - 1}}$)

A. 97 Hz
B. 100 Hz
C. 103 Hz
D. 106 Hz

Answer 1

It is given that the source of sound is in motion with respect to the observer in the direction making an angle 60° with the line joining the source and the observer. So there will be a change in the frequency of the sound observed by the observer due to Doppler’s effect. To find the frequency detected by the observer we use the Doppler’s effect.

Formula used:
${f_{ap}} = {f_o}\left( {\dfrac{{v \pm {v_o}}}{{v \pm {v_s}}}} \right)$
where ${f_{ap}}$ is the apparent frequency heard by the listener moving with speed ${v_o}$ with respect to the source which is moving with speed ${v_s}$, ${f_o}$ is the original frequency and v is the speed of sound in air

Complete step by step solution:

Figure: The source of sound and the observer.

The original frequency of the sound emitted from the source is 100 Hz. It is given that the source is moving with constant velocity $19.4m/s$ in the direction making 60° with the line joining the source and the stationary observer. The speed of sound in still air is given as 330 m/s.

The component of the velocity of the source along the line joining the source and stationary observer will be,
${v_s} = \left( {19.4\,m/s} \right)\cos 60^\circ = 9.70\,m/s$
The speed of the observer is zero as it is at rest. So, using the Doppler’s effect the apparent frequency of the sound detected by the observer will be,
$f' = {f_o}\left( {\dfrac{v}{{v - {v_s}}}} \right) \\\$
Putting the values, we get
$f' = \left( {100Hz} \right)\left( {\dfrac{{330}}{{330 - 9.7}}} \right) \\\$
$\Rightarrow f' = \left( {100Hz} \right) \times \left( {\dfrac{{330}}{{320.3}}} \right) \\\$
$\therefore f' = 103\,Hz$
Hence, the apparent frequency observer by the stationary observer is 103 Hz.

Therefore, the correct option is C.

Note: We should be careful while taking the velocity of the source of the sound and the observer in Doppler’s effect because the velocity component along the line joining the source and the observer is used for the Doppler’s effect formula. The perpendicular component of the velocity doesn’t have an effect on the change in frequency due to Doppler’s effect.