Question

A source of light is hung $h\text{ mts}$, directly above a straight horizontal path on which a boy
‘$\text{a}$’ mts., in height is walking. If a boy walks at a rate of $b\text{ mts/sec}$ from the light then the rate at which his shadow increases
$\text{(A) }\dfrac{ab}{h-a}\text{mts/sec}$
$\text{(B) }\dfrac{ab}{h+a}\text{mts/sec}$
$\text{(C) }\dfrac{ab}{2(h-a)}\text{mts/sec}$
$\text{(D) }\dfrac{ab}{2(h+a)}\text{mts/sec}$

Answer 1

for these types of questions, we should draw diagrams to understand clearly. We will use properties of similarity of triangles which is that sides of two similar triangles are always in proportion. Also, we will use derivatives for calculating the rate of change.

Complete step-by-step solution
Let us consider the following diagram for understanding the question properly.

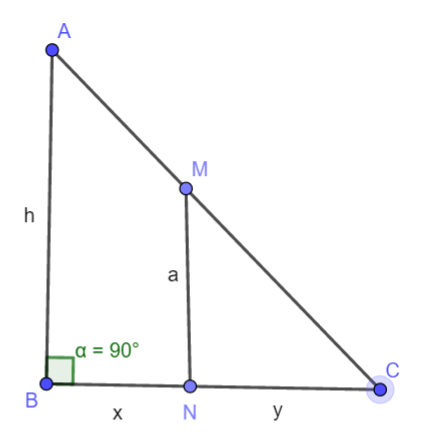
In the diagram, we have considered A as the source of light which is at $h\text{ }mts$. Above the ground forming the side of the triangle as AB with length ‘ $h$’. MN is represented as a boy with height $\text{a mts}$. We have considered NC as the length of the shadow. Let $\text{NC =y units}$. Also, we have considered distance from the AB to the boy as ‘ $x\text{ }mts$’. From the diagram, we can clearly see that it forms two triangles ABC and MNC. Since AB and MN are both perpendicular to the ground. Therefore, $\angle ABC=\angle MNC={{90}^{\circ }}$.
$\angle ACB$ is common to both triangles. As we know light sources form the same angle as the boy, therefore, $\angle BAC$is equal to $\angle NMC$. Therefore, $\vartriangle ABC$ and $\vartriangle MNC$ are similar to the SSS criteria of similarity.
We are given,

& AB=h\text{ mts} \\\ & \text{MN= a mts} \\\ \end{aligned}$$ As boy walks at rate of $$b\text{ mts/sec}$$, therefore we can write the rate at which boy walks can write the rate at which boy walks by $$\dfrac{dx}{dt}$$ where $$dx$$ is rate at which boy is moving on horizontal path and $$dt$$ is rate at which time is passing. Hence, $$\dfrac{dx}{dt}=b\text{ mts/sec}$$……equation (1) Since, $$\vartriangle ABC$$ and $$\vartriangle MNC$$ are similar, so their sides are proportional which is given as, $$\Rightarrow \dfrac{AB}{MN}=\dfrac{BC}{NC}=\dfrac{AC}{MC}$$ Taking first two terms, $$\Rightarrow \dfrac{AB}{MN}=\dfrac{BC}{NC}$$ From the diagram, it is clear that $$AB=h\text{ }$$,$$\text{MN= a}$$, $$BC=BN+NC=x+y$$ and $$NC=y$$. Hence, putting value is above equation, we get, $$\dfrac{h}{a}=\dfrac{x+y}{y}$$ Cross multiplying, we get, $$hy=a(x+y)$$ $$\Rightarrow hy=ax+ay$$ $$\Rightarrow hy-ay=ax$$ $$\Rightarrow y(h-a)=ax$$ $$\Rightarrow y=\dfrac{ax}{h-a}$$ Taking derivative on both side with respect to $$x$$, we find, $$\dfrac{dy}{dt}=\dfrac{d}{dt}(\dfrac{ax}{h-a})$$ $$\Rightarrow\dfrac{dy}{dt}=\dfrac{a}{h-a}.\dfrac{dx}{dt}$$ Putting value of equation (1) in above equation, we get $$\dfrac{dy}{dt}=\dfrac{a}{h-a}.(b)$$ $$\Rightarrow \dfrac{dy}{dt}=\dfrac{ab}{h-a}$$ As rate of increase in shadow is given by $$\dfrac{dy}{dt}$$, Therefore, the rate at which shadow increases = $$=\dfrac{ab}{h-a}mts/\sec $$. **Hence, option (a) is correct.** **Note:** Students should carefully draw the diagram for these types of questions. Students should not get confused about finding the length of shadow or rate at which shadow increases. For length, we have to find the value of $$\dfrac{dy}{dt}$$. Students should also check units properly.