Question

A solution contains 1 millicurie of L-phenylalanine $^{{\mathbf{14}}}{\mathbf{C}}$(uniformly labelled) in $2.0$ mL solution. The specific activity of the labelled sample is given as 150 millicuries/mmol. The activity of the solution in terms of counting per minute/mL at a counting efficiency of 80% is :
A. $88.8 \times {10^7}{\text{cpm/L}}$
B. $88.8 \times {10^6}{\text{cpm/mL}}$
C. $88.8 \times {10^5}{\text{cpm/mL}}$
D. $88.8 \times {10^7}{\text{cpm/mL}}$

Answer 1

To answer this question, you should recall the concept of the specific activity of a labelled sample. The specific activity can be defined as the activity per quantity of a radionuclide and it is a physical property of that radionuclide.

Formula used: ${\text{molarity}} = \dfrac{{{\text{moles (in mmol)}}}}{{{\text{V (in mL)}}}}$

Complete Step by step solution:
To answer this question let us first calculate the concentration of the given labelled sample.
(a) 1 mmole = 150 millicurie, using unitary method
1 millicurie=$\dfrac{1}{{150}}$ mmol
Now, concentration can be calculated by dividing the moles with the given volume
${\text{molarity}} = \dfrac{{{\text{moles (in mmol)}}}}{{{\text{V (in mL)}}}} = \dfrac{1}{{150 \times 2}} = 3.33 \times {10^{ - 3}}{\text{M}}$​
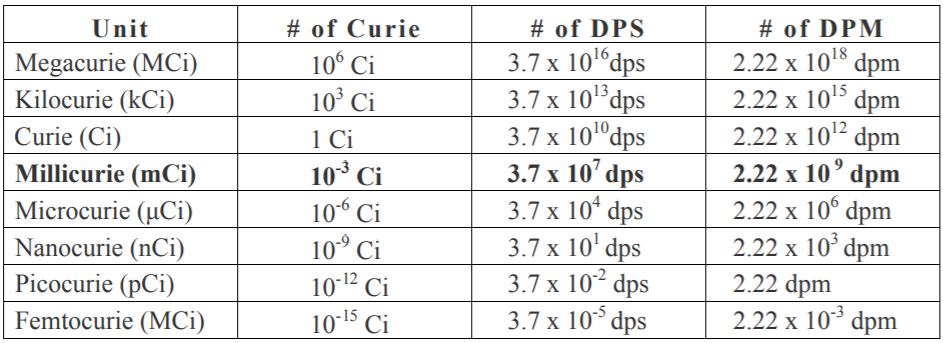
b) We know that 1 curie = $3.7 \times {10^{10}}{\text{dps}}$= $3.7 \times {10^{10}} \times 60{\text{ dpm}}$ . This can be converted to counting per minute:
$\Rightarrow 3.7 \times {10^{10}} \times 60 \times \dfrac{{80}}{{100}}$ counting per minute
$\therefore$ 1 millicurie = $3.7 \times {10^{10}} \times 60 \times \dfrac{{80}}{{100}} \times {10^{ - 3}}{\text{cpm}}$.
To achieve the final answer we need to divide this value with volume.
$\Rightarrow 3.7 \times {10^{10}} \times 60 \times \dfrac{{80}}{{100}} \times {10^{ - 3}} \times \dfrac{1}{2}$
$\Rightarrow 88.8 \times {10^7}{\text{cpm/mL}}$
Therefore, we can conclude that the correct answer to this question is option D.

Additional information: The emissions in most of the spontaneous radioactive decays involve alpha $(\alpha )$particle, the beta $(\beta )$ particle, the gamma-ray, and the neutrino. The alpha particle is the nucleus of doubly charged ${\text{He}}_2^4$. Beta particles can be beta minus beta plus. Beta minus is an electron created in the nucleus during beta decay. Beta plus particle is also known as a positron, is the antiparticle of the electron; when brought together, two such particles will mutually annihilate each other.

Note: To answer the questions related to radioactivity you need to know the important conversion units regarding the disintegration of a radioactive compound.