Solveeit Logo
Login

Question

Question: A solid uniform ball having volume V and density \[\rho \] floats at the interface of two immiscible...

A solid uniform ball having volume V and density ρ\rho floats at the interface of two immiscible liquids as shown in figure. The densities of the upper and the lower liquids are ρ1{\rho _1} and ρ2{\rho _2} respectively, such that ρ1<ρ<ρ2{\rho _1} < \rho < {\rho _2}. What fraction of the volume of the ball will be in the lower liquid:-
A. ρ−ρ2ρ1−ρ2\dfrac{{\rho - {\rho _2}}}{{{\rho _1} - {\rho _2}}}
B. ρ1ρ1−ρ2\dfrac{{{\rho _1}}}{{{\rho _1} - {\rho _2}}}
C. ρ1−ρρ1−ρ2\dfrac{{{\rho _1} - \rho }}{{{\rho _1} - {\rho _2}}}
D. ρ1−ρ2ρ2\dfrac{{{\rho _1} - {\rho _2}}}{{{\rho _2}}}

Explanation

Solution

Hint: We know that when a body is immersed in a fluid it experiences an upward force called buoyant force which is equal to the weight of the fluid displaced by the body.

Complete step-by-step answer:

Formula used –

  1. For a stationary body in a fluid, buoyant force=weight of the body immersed.
  2. Force acting on the body immersed in the fluid, F=VρgF = V\rho g

Given, Volume of the body=V
Density of the body=ρ\rho
Density of upper liquid=ρ1{\rho _1}
Density of lower liquid= ρ2{\rho _2}

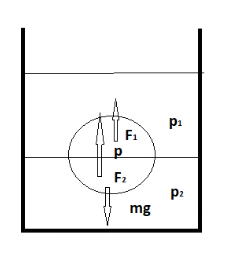
Let the volume of the body in upper liquid be v1{v_1} and the volume in lower liquid be v2{v_2}.
V=v1{v_1}+v2{v_2}
Since the ball is stationary at the interface, therefore the net buoyant force on the body is equal to the weight of the body.

Let the buoyant force due to upper liquid be F1{F_1}and due to the lower liquid be F2{F_2}.

F1{F_1}+F2{F_2}=mg…..(i)
F1=v1ρ1g{F_1} = {v_1}{\rho _1}g
And F2=v2ρ2g{F_2} = {v_2}{\rho _2}g
Putting these in equation (i)
v1ρ1g+v2ρ2g=(v1+v2)ρg{v_1}{\rho _1}g + {v_2}{\rho _2}g = ({v_1} + {v_2})\rho g
Eliminating g on both sides, we get
v1ρ1+v2ρ2=v1ρ+v2ρ{v_1}{\rho _1} + {v_2}{\rho _2} = {v_1}\rho + {v_2}\rho
v1ρ1+(V−v1)ρ2=v1ρ+(V−v1)ρ v1(ρ1−ρ2)+Vρ2=v1(ρ−ρ)+Vρ v1(ρ1−ρ2)=V(ρ−ρ2) v1V=(ρ−ρ2)(ρ1−ρ2) v2V=1−v1V=1−(ρ−ρ2)(ρ1−ρ2) v2V=ρ1−ρρ1−ρ2  {v_1}{\rho _1} + (V - {v_1}){\rho _2} = {v_1}\rho + (V - {v_1})\rho \\\ {v_1}({\rho _1} - {\rho _2}) + V{\rho _2} = {v_1}(\rho - \rho ) + V\rho \\\ {v_1}({\rho _1} - {\rho _2}) = V(\rho - {\rho _2}) \\\ \dfrac{{{v_1}}}{V} = \dfrac{{(\rho - {\rho _2})}}{{({\rho _1} - {\rho _2})}} \\\ \dfrac{{{v_2}}}{V} = 1 - \dfrac{{{v_1}}}{V} = 1 - \dfrac{{(\rho - {\rho _2})}}{{({\rho _1} - {\rho _2})}} \\\ \dfrac{{{v_2}}}{V} = \dfrac{{{\rho _1} - \rho }}{{{\rho _1} - {\rho _2}}} \\\

Hence the correct option is C.

Note: The buoyant force on a body immersed is equal to the weight of the fluid displaced and for a stationary body both the buoyant force and weight of the body should be equal and balanced.