Question
Question: A solid sphere rolls down on two inclined planes of the same heights but different angles of inclina...
A solid sphere rolls down on two inclined planes of the same heights but different angles of inclination. (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
Solution
Hint: This problem uses the concept of circular motion along an inclined plane, which is a combination of both translational and rotational motions for the rolling case. Hence, the total energy of the sphere when it rolls down an inclined plane is 21mv2+21Iω2. This energy will be equal to the potential energy, mgh. Further, equating the forces using mgsinθ−f=ma and Iα=fr, we can find the acceleration (a) value for each case of different angles of inclination (θ). Then, we will use Newton's law of motion formula of: s=ut+21at2 to find the time of travel (t).
Step by step solution:
Let’s start by making a diagram of the problem.
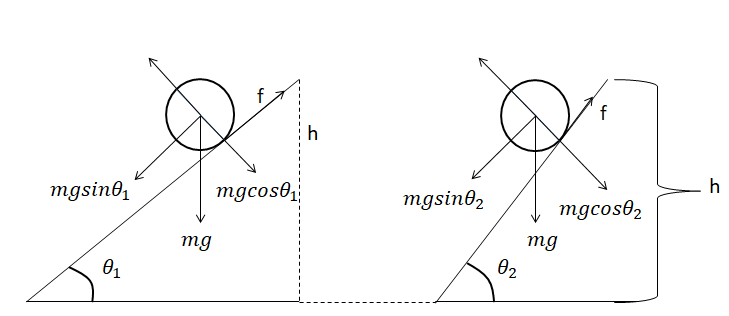
We have two different inclined planes having angles of inclination θ1 and θ2. Consider the sphere of mass (m) and radius (r) to be released from height (h). Hence, the potential energy of the sphere is given by PE=mgh. As the sphere rolls down the inclined plane, hence the potential energy of the sphere gets converted into both translational and rotational motion. Therefore, the total potential energy of the sphere gets completely converted into the translational and rotational motion21mv2+21Iω2. Using this relation we get, mgh=21mv2+21Iω2. Using the relation of v=ωr⇒ω=rv and substituting the value of moment of Inertia of a sphere, which is I=52mr2 into the above equation: mgh=21mv2+21Iω2⇒mgh=21mv2+21(52mr2)(rv)2⇒gh=21v2+51v2⇒gh=107v2.
Therefore, the velocity of the sphere will be: v=710gh. Since, the value of velocity is independent of the angle of inclination(θ), hence both the spheres will reach the bottom of the plane with same speed.
For case (b), we will consider the free body diagram made above. We will solve the problem for one angle of inclination as the solution will be the same for the other angle of inclination.
We will solve for the angle of inclination (θ1). Here, we will consider the net tangential acceleration for this system given by (a1). Hence the two equations of force we will get are:
mgsinθ1−f=ma1→(1), where f is the frictional force acting at the point of contact in between the sphere and the plane.
Iα=fr→(2), where the angular acceleration is given by: α=ra1. We also know that the moment of Inertia of the sphere is: I=52mr2. Hence, the equation (2) becomes, 52mr2(ra1)=fr⇒52ma1r=fr⇒52ma1=f. Substituting in the value of the frictional force into equation (1), we get: mgsinθ1−52ma1=ma1⇒mgsinθ1=57ma1⇒75gsinθ1=a1.
Similarly, the tangential acceleration (a2) will be: 75gsinθ2=a2.
The incline distance travelled by the sphere in each case is given by: s=sinθh. Hence, the amount of inclined distance travelled in each case is:s1=sinθ1h and s2=sinθ2h.
Using the newton’s law of motion of s=ut+21at2 and putting in the values of (s) and (a) for each case, we will find the value of t. u=0, since the sphere is initially at rest.
Therefore,s1=sinθ1h=21a1t12⇒sinθ1h=21(75gsinθ1)t12⇒t12=5g14h(sin2θ11)⇒t1=sinθ115g14h.
Similarly, t2=sinθ215g14h.
Therefore, the time taken by the sphere in each case is different. We know that in the interval of 00 to 900, sine function is increasing and from the figure θ1<θ2. Since t∝sinθ1, therefore the time taken by the sphere to roll down the inclined plane having inclination angle θ1 is larger than the time taken by the sphere to roll down the inclined plane by the sphere having an inclination angle of θ2 for θ1<θ2.
Note: A shortcut to solving this problem is by taking the values of the tangential accelerations: a1=75gsinθ1 and a2=75gsinθ2. Hence, a∝sinθand since no external force is applied the sphere having higher acceleration will roll down faster. Since, θ1<θ2, therefore a1<a2. Hence, the sphere having an inclination angle θ1 is roll down slower than the one rolling down the inclined plane having an inclination angle of θ2.
