Question

A solid sphere of uniform density and radius $R$ exerts a gravitational force of attraction${F_1}$, on the particle $P$, distance $2R$ from the centre of the sphere. A spherical cavity of radius $R/2$ is now formed in the sphere as shown in figure. The sphere with cavity now applies a gravitational force ${F_2}$, on the same particle P. Find the ratio $\dfrac{{{F_1}}}{{{F_2}}}$.

Answer 1

Hint: The Force due to remaining portion is Force due to (A) - Force due to (B). Masses of the spheres can be found using their volumes and density. Use the Universal Law of gravitation: $F = \dfrac{{GMm}}{{{R^2}}}$, which gives the force between two masses $M$and $m$separated by a distance $R$

Complete step by step solution:

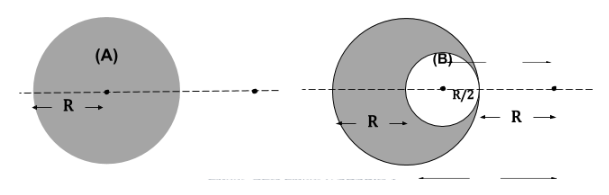
We know that the total gravitational force at a point is the vector sum of gravitational forces from individual masses.

A solid body as in figure can be imagined to be made up of many tiny individual masses.
So the net gravitational force at P due to all these masses can be calculated as:

${F_{net}} = \sum\limits_{all} {{F_i}} = \sum\limits_{all} {\dfrac{{G{m_i}m}}{{{r_i}^2}}}$
Now if, as in question, a sphere is cut out from the initial object, we can easily find the force at $P$ due to the rest of the mass in the following way:

Let us first use separate identities for the masses that are going to be cut out.
Let's say the masses that are going to get removed are represented as ${m_j}$ and let their position from P be ${r_j}$

For the rest of the object, we use ${m_i}$ for individual masses and ${r_i}$ for their position from $P$

Now if the sphere was not removed, the Gravitational force at P would have been :
${F_{net}} = \sum\limits_{all} {{F_i}} = \sum\limits_i {\dfrac{{G{m_i}m}}{{{r_i}^2}} + \sum\limits_j {\dfrac{{G{m_j}m}}{{{r_j}^2}}} }$

Since this is the force due to whole sphere, we know it would be${F_{net}} = \dfrac{{G{M_A}m}}{{{R_1}^2}}$.

Also, the second sum $\left( {\sum\limits_j {\dfrac{{G{m_j}m}}{{{r_j}^2}}} } \right)$ is the force exerted by the smaller sphere (B) at P. We know this Force as ${F_{net}} = \dfrac{{G{M_B}m}}{{{R_2}^2}}$ where ${R_2}$ is the distance from Centre of Sphere to P

That means: ${F_{net}} = \dfrac{{G{M_A}m}}{{{R_1}^2}} = \sum\limits_i {\dfrac{{G{m_i}m}}{{{r_i}^2}} + \dfrac{{G{M_B}m}}{{{R_2}^2}}}$

We are asked to find the Force exerted by the remaining portion, which is the first sum $\left( {\sum\limits_i {\dfrac{{G{m_i}m}}{{{r_i}^2}}} } \right)$. Let’s call this $F$.

.Rearranging equation (1) gives :

$\sum\limits_i {\dfrac{{G{m_i}m}}{{{r_i}^2}} = \dfrac{{G{M_A}m}}{{{R_1}^2}} - } \dfrac{{G{M_B}m}}{{{R_2}^2}}$

$F = \sum\limits_i {\dfrac{{G{M_A}m}}{{{R_1}^2}} - } \dfrac{{G{M_B}m}}{{{R_2}^2}}$

So we just verified that we can subtract the Force due to a smaller sphere (B) from that due to the Total Sphere (A) to get the force exerted by the remaining portion.

Now Let’s answer the question

Since the spheres have a constant density, we can find the mass of smaller and larger spheres.

The mass of initial Sphere (A) :

$\rho \dfrac{4}{3}\pi {R^3} = M(say)$

and similarly, that of The cut out sphere (B) would be

$\rho \dfrac{4}{3}\pi {\left( {R/2} \right)^3} = \dfrac{M}{8}$

Now, as we have seen,

Gravitational force at P after cutting = Force due to (A) - Force due to (B).

Force due to (A)

${F_A} = \dfrac{{G{M_A}m}}{{{R_1}^2}} = \dfrac{{GMm}}{{{{(2R)}^2}}} = \dfrac{1}{4}\dfrac{{GMm}}{{{R^2}}}$

Force due to (B)

${F_B} = \dfrac{{G(M/8)m}}{{{{(3R/2)}^2}}} = \dfrac{1}{{18}}\dfrac{{GMm}}{{{R^2}}}$

So Force due to cut out portion is :

${F_A} - {F_B} = \dfrac{1}{4}\dfrac{{GMm}}{{{R^2}}} - \dfrac{1}{{18}}\dfrac{{GMm}}{{{R^2}}} = \dfrac{7}{{36}}\dfrac{{GMm}}{{{R^2}}}$

According to the question, ${F_1}$ is the Force exerted by sphere (A).

So ${F_1} = {F_A}$

${F_2}$ is the force exerted by The remaining portion.

${F_2} = {F_A} - {F_B}$

So the required ratio :

$\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{F_A}}}{{{F_A} - {F_B}}} = \dfrac{{\left( {\dfrac{1}{4}\dfrac{{GMm}}{{{R^2}}}} \right)}}{{\left( {\dfrac{7}{{36}}\dfrac{{GMm}}{{{R^2}}}} \right)}} = \dfrac{9}{7}$, which is the correct solution.
.
Note: Similar argument of splitting the sum can be applied in questions where Moment of inertia or the Electric Potential of a cut out shape is asked.
Also, grouping similar quantities and giving it some name saves a lot of writing in questions involving ratios. For example $\rho \dfrac{4}{3}\pi {R^3} = M(say)$ ; ${F_A} = \dfrac{1}{4}\dfrac{{GMm}}{{{R^2}}} = \dfrac{1}{4}f(say)$