Question

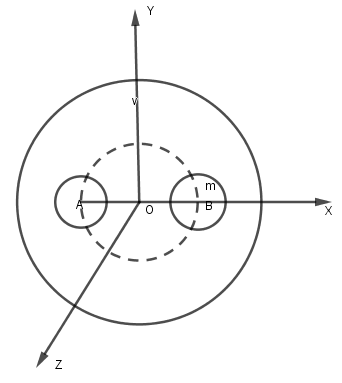
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two spheres of equal radii 1 unit, with their centres at A(−2,0,0) and B(2,0,0), respectively, are taken out of the solid leaving behind spherical cavities as shown in the figure. Then,
(A) The gravitational force due to this object at the origin is zero
(B) The gravitational force at the point B(2,0,0) is zero
(C) The gravitational force is same at all the points on the circle of the circle ${y^2} + {z^2} = 36$
(D) The gravitational force is same at all the points on the circle of the circle ${y^2} + {z^2} = 4$

Answer 1

According to question, we have to find out which of the following options are correct. In this question we need to apply the superposition principle, which states that, net gravitational field at a point is the vector sum of the gravitational fields at that point due to different sources.

Complete step by step answer:
First we need to understand terms like gravitational force and gravitational potential. Gravitational force is the force of attraction between all masses in the universe; especially the attraction of the earth's mass for bodies near its surface. Gravitational potential is the gravitational potential at a location equal to the work per unit mass that would be needed to move an object to that location from a fixed reference location.
According to question,
Let ${F_A}$ = Gravitational force due to sphere A
${F_B}$ = Gravitational force due to sphere B
${F_R}$ = Gravitational force due to the remaining portion after the cavities are removed
Now according to the superposition principle we can say that ${F_A} + {F_B} + {F_R} = 0$ as the force due to the centre sphere is zero at centre.
Due to symmetry we can say that ${F_A} + {F_B} = 0$ and thus we can say that ${F_R} = 0$ , so option (A) is correct.
Now coming on (B),
Field due to entire sphere is given by $\overrightarrow F = \dfrac{{GM}}{{{R^3}}}r$
$\overrightarrow F = \dfrac{{GM}}{{64}}2$ = $\dfrac{{GM}}{{32}}$
Also, $\overrightarrow {{F_A}} = \dfrac{{GM}}{{{4^2}}} = \dfrac{{GM}}{{16}}$
$\overrightarrow {{F_A}} = \dfrac{{GM}}{{16 \times 64}} = \dfrac{{GM}}{{1024}}$
Here M is the mass of A = $\dfrac{M}{{64}}$ and $\overrightarrow {{F_B}} = 0$
For superposition principle we have ${F_A} + {F_B} + {F_R} = F$
From here we can say that, $\overrightarrow {{F_R}} = \overrightarrow F - \overrightarrow {{F_A}}$ $= \dfrac{{GM}}{{32}}\widehat i$
$\dfrac{{GM}}{{104}}\widehat i = \dfrac{{31GM}}{{104}}\widehat i \ne 0$
Hence option (B) is not correct regarding potential at point on ${y^2} + {z^2} = 36$ . We can see that the radius of the circle is 6 units, now all the points on it are symmetrical, located from the remaining sphere. Potential is also the same at every point on the circle. Hence potential must be the same at every point on the circle as the same logic holds for ${y^2} + {z^2} = 4$ so option (C) and (D) are also correct.
Thus, (A), (C) and (D) correct.

Note:
Be careful while applying the conditions given in the question. While solving the question, keep in mind the concept of superposition principle. Calculation mistakes are possible, so try to avoid them. We must remember that Gravitational potential is the gravitational potential at a location equal to the work per unit mass that would be needed to move an object to that location from a fixed reference location. Also, students must remember the value of gravitational constant G.