Question

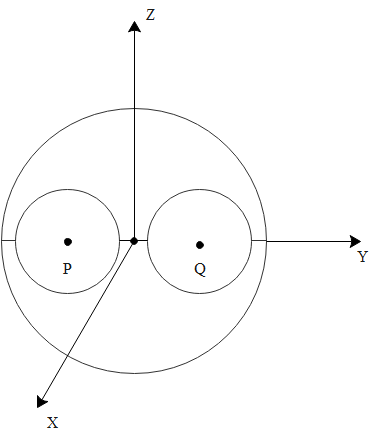
A solid sphere of uniform density and mass M has radius 4 m. Its centre is at the origin of the coordinate system. Two spheres of radii 1 m are taken out so that their centres are at P (0, —2, 0) and Q (0, 2, 0) respectively. This leaves two spherical cavities.
What is the gravitational field at point P?

$\begin{aligned} & A)\dfrac{31GM}{1024} \\\ & B)\dfrac{31Gm}{1024} \\\ & C)31GM \\\ & D)\text{Zero} \\\ \end{aligned}$

Answer 1

We must be aware of the basics of what is the gravitational field. The gravitational field is basically the region of space that surrounds a body in which force of gravitational attraction is experienced by another body. We should consider the gravitational field as the gravitational force which is exerted per unit mass on small mass at any point in the body. With this theory in mind, we will be able to solve the given question.

Complete step-by-step solution:
We know that if the cavities are not made then the intensity at the point P (or even Q) by the total sphere will be,
${{I}_{R}}=\dfrac{GM}{{{R}^{3}}}x=\dfrac{GM}{64}\times 2=\dfrac{GM}{32}$
Here, ${{I}_{R}}$ is the intensity of the gravitational field due to the whole sphere.
$R$ is the radius of the big sphere.
$M$ is the mass of the big sphere.
But, we can also define the intensity of the gravitational field due to the whole sphere as the sum of intensities of gravitational fields due to 3 spheres when two 1m radius spheres are cut from it.
$\Rightarrow {{\overrightarrow{I}}_{R}}=\overrightarrow{{{I}_{P}}}+\overrightarrow{{{I}_{Q}}}+\overrightarrow{I}$
Here, ${{I}_{R}}$ is the intensity of the gravitational field due to the whole sphere.
$\overrightarrow{{{I}_{P}}}$ is the intensity of the gravitational field due to sphere P.
$\overrightarrow{{{I}_{Q}}}$ is the intensity of the gravitational field due to sphere Q.
$\overrightarrow{I}$ is the intensity of the gravitational field due to the remaining portion of the sphere.
So, from the above equation, we can write that,
$\overrightarrow{I}=\overrightarrow{{{I}_{R}}}-\overrightarrow{{{I}_{P}}}-\overrightarrow{{{I}_{Q}}}$
Now, let us take the density of the big sphere as $d$. It will be the same for the smaller spheres taken out from it.
We know, $\text{density}=\dfrac{\text{mass}}{\text{volume}}$
And the volume of a sphere is given as $V=\dfrac{4}{3}\pi {{R}^{3}}$ .
Therefore, the mass of the big sphere $M=\dfrac{4\pi \times {{\left( 4 \right)}^{3}}d}{3}$ .
The mass of the small sphere P and Q will be $m=\dfrac{4\pi {{\left( 1 \right)}^{3}}d}{3}$ .
Where, $d$is the density of the sphere.
Now, on comparing both masses, we can write that $m=\dfrac{M}{64}$.
Now at the point P,
${{I}_{P}}$ is zero.
Because, ${{I}_{P}}$ is given as $\dfrac{Gm}{{{r}^{2}}}$. But at point P, $r\to 0$ .
$\Rightarrow {{I}_{P}}=0$

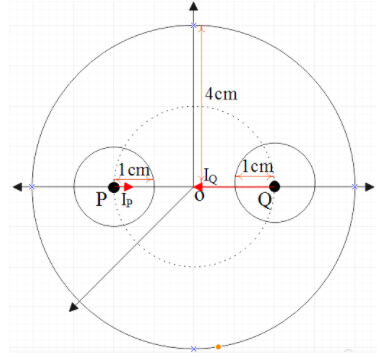
Now, the value of ${{I}_{Q}}$ at P will be,
${{I}_{Q}}=\dfrac{Gm}{{{r}^{2}}}$
Now we have to put the values in the above equation.
From the figure, we can understand that $r=4cm$.
So we can write that ${{I}_{Q}}=\dfrac{G}{{{4}^{2}}}(\dfrac{M}{64})=\dfrac{31GM}{1024}$
Hence the correct answer to the equation is Option A.

Note: In case of such type of questions, we must consider the geometry of the given diagram. Geometry is highly important as it will determine the point where the gravitational field is high. Moreover, the coordinate system creates a major impact on the gravitational field because shapes can determine if the gravitational field lies inside or outside the given body.