Question

A solid sphere of radius R and density $\rho$ is attached to one end of a massless spring of force constant k. The other end of the spring of radius R and density $3\rho$. The complete arrangement is placed in a liquid of density $2\rho$ and is allowed to reach equilibrium. The correct statement(s) is (are).
A) the net elongation of the spring is $\dfrac{{4\pi {R^3}\rho g}}{{3k}}$.
B) the net elongation of the spring is $\dfrac{{8\pi {R^3}\rho g}}{{3k}}$.
C) the light sphere is partially submerged.
D) the light sphere is completely submerged.

Answer 1

The spring force depends upon the spring constant k, the density of the body is the ratio of mass and volume. When a body emerges in the liquid then the liquid applies a force in the up direction and the net weight of the body decreases.

Complete step by step answer:
There are two spheres at the two ends of the spring and this whole system is placed in the liquid of density $2\rho$.
The liquid will apply an upwards force which is the buoyancy force on the two spheres.

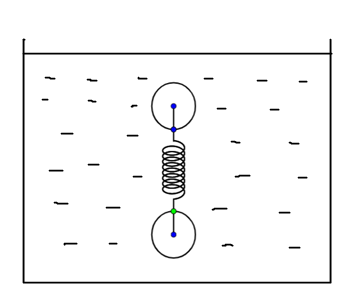
The tension in the string is in the upward direction, the buoyancy force is in the upwards direction, and the weight of the spheres in the downwards direction.

In the equilibrium position, the relation that we get is,
$T + B = W$
So now let us calculate the total weight of the sphere of density $3\rho$ also the spring is massless.
$\Rightarrow W = \dfrac{4}{3}\pi {R^3}\left( {3\rho g} \right)$
The buoyancy force on the sphere is given by,
$\Rightarrow B = \dfrac{4}{3}\pi {R^3}\left( {2\rho g} \right) + \dfrac{4}{3}\pi {R^3}\left( {2\rho g} \right)$
$\Rightarrow B = 2 \cdot \left[ {\dfrac{4}{3}\pi {R^3}\left( {2\rho g} \right)} \right]$
$\Rightarrow B = 4 \cdot \left[ {\dfrac{4}{3}\pi {R^3}\left( {\rho g} \right)} \right]$
Since in equilibrium position the forces on the sphere will be,
$\Rightarrow T + B = W$
$\Rightarrow T = W - B$
$\Rightarrow T = \dfrac{4}{3}\pi {R^3}\left( {3\rho g} \right) - 4 \cdot \left[ {\dfrac{4}{3}\pi {R^3}\left( {\rho g} \right)} \right]$
$\Rightarrow T = \dfrac{4}{3}\pi {R^3}\left( {3\rho g} \right) - \left[ {\dfrac{4}{3}\pi {R^3}\left( {2\rho g} \right)} \right]$
$\Rightarrow T = \dfrac{4}{3}\pi {R^3}\left( {\rho g} \right)$
As the spring has a spring force which is equal to the tension in the spring, therefore,
$F = T$
$\Rightarrow F = \dfrac{4}{3}\pi {R^3}\left( {\rho g} \right)$
$\Rightarrow k \cdot x = \dfrac{4}{3}\pi {R^3}\left( {\rho g} \right)$ (where k is the spring constant and x is the elongation in the spring).
So the elongation of the spring is given by,
$\Rightarrow x = \dfrac{4}{{3 \cdot k}}\pi {R^3}\left( {\rho g} \right)$
The light sphere will also be completely submerged in the liquid as the tension of the spring is more than the buoyancy force on the light sphere.

Therefore, the correct option for this problem is option A and option D.

Note:
The tension in the spring is equal to the spring force on the spring; they both are equal. When a body is submerged completely or partially then a buoyancy force acts on the body which results in a decrease in the weight of the body.