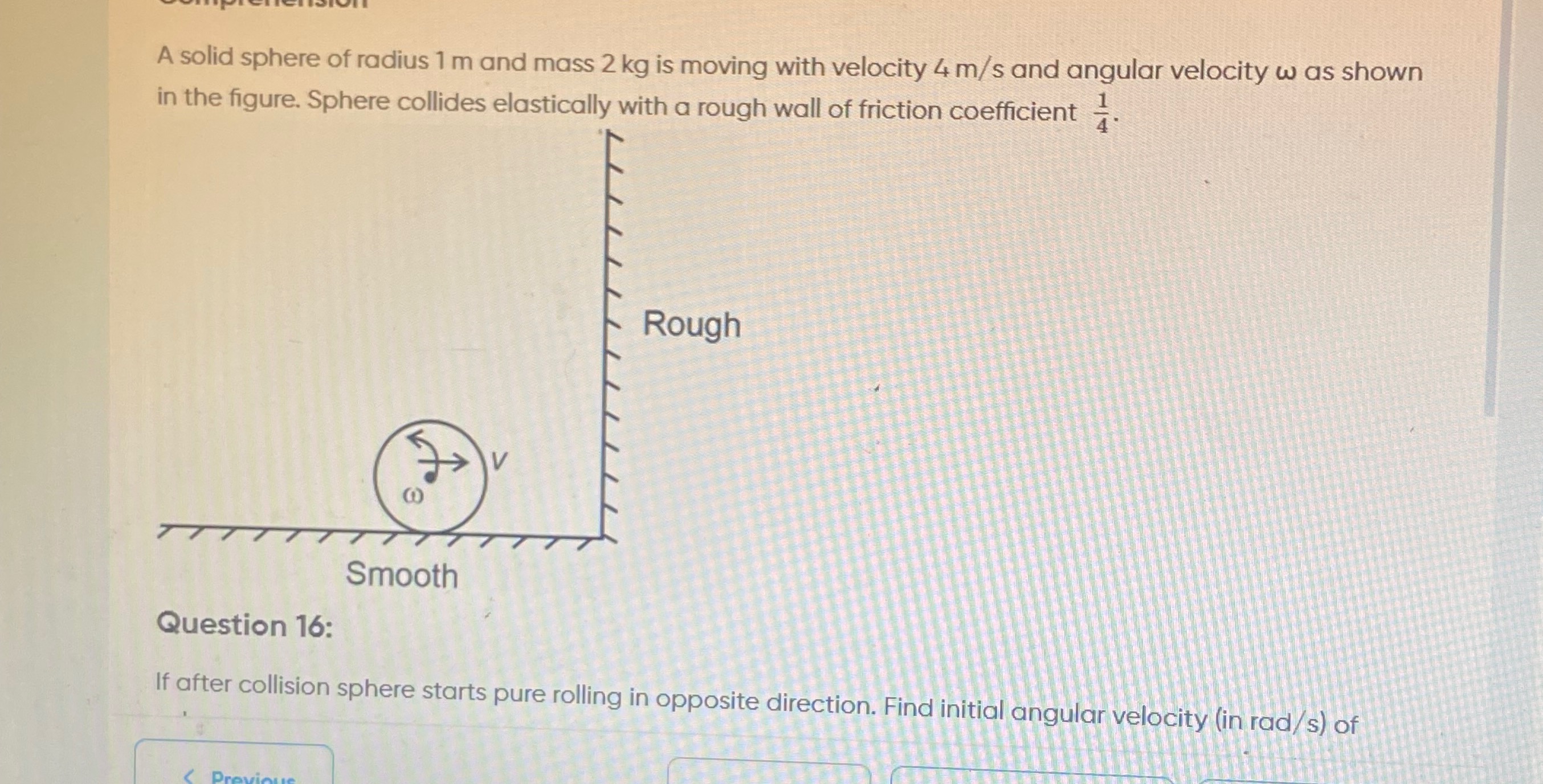
Question: If after collision sphere starts pure rolling in opposite direction. Find initial angular velocity (...

Question

If after collision sphere starts pure rolling in opposite direction. Find initial angular velocity (in rad/s) of

Answer 1

Solution

We take the following sign‐convention:

Positive x–direction is to the right.
For rotation about the centre, we define ω positive if it is counterclockwise.

Recall that for a sphere rolling without slipping on a horizontal floor the “no–slip” condition is obtained by requiring that the instantaneous velocity of the point of contact vanish. With the centre moving with speed v and the sphere of radius r the velocity at the contact (located a distance r directly downward from the centre) is

v + (ω × (–rĵ)).

A short calculation shows that the no–slip condition leads to

v + rω = 0 (1)

provided we interpret ω as a “signed” scalar (note: if the sphere rolls to the right, then v>0 and the sphere must rotate clockwise; since clockwise means ω<0, (1) gives ω = –v. Similarly, if it rolls to the left, v<0 and then ω = –v is positive).

In our problem the sphere is on a smooth horizontal floor and collides with a vertical wall. (The sphere is simultaneously in contact with floor and wall — the wall is “rough” so that it can supply an impulse of friction.) Before collision the sphere has a centre–of–mass speed vᵢ = +4 m/s (to the right) and an angular speed ω (unknown). Since the pure rolling condition for motion to the right would require ω = –4, we see that in general the sphere is “slipping” (its spin is not enough to roll without slipping).

During the brief collision the wall exerts:

a normal (horizontal) impulse which reverses the centre–of–mass motion, and
a friction impulse (vertical) which changes the spin.

Since the wall is fixed the collision is elastic in the normal direction so that

v_f = –4 m/s (the centre–of–mass speed is unchanged in magnitude but reversed).

On the floor immediately after collision the sphere is observed to roll without slipping. Now note that after the collision the sphere moves to the left (v_f < 0) and pure rolling requires (by similar reasoning as above) that

v_f + rω_f = 0 → ω_f = –v_f.

Thus here

ω_f = –(–4) = +4 rad/s. (2)

Let I be the moment of inertia of the solid sphere about its centre. We have

I = (2/5) m r².

With m = 2 kg and r = 1 m we get

I = (2/5)×2 = 4/5 kg·m².

The friction impulse, J_f, acting at the wall (which, being “rough”, is able to exert friction) produces a change in the sphere’s angular momentum about its centre. Namely,

I (ω_f – ω) = (lever arm)×J_f.

Here the lever arm is r = 1 m so that

I (ω_f – ω) = J_f. (3)

However the friction impulse cannot be arbitrarily large. In an oblique collision its maximum magnitude is determined by the coefficient of friction μ and the normal impulse J_n. (For a fixed wall the normal impulse is determined solely by the reversal of the centre–of–mass momentum.) In the horizontal direction we have

m (v_f – v) = –J_n.

The change in horizontal momentum is

2 (–4 – 4) = –16 (N·s),

so that

J_n = 16 N·s.

Thus the maximum available friction impulse is

J_f(max) = μ J_n = (1/4)×16 = 4 N·s. (4)

For the ball to “just” come out rolling without slipping, the friction impulse must be able to supply the required change in spin. Hence we set

I (ω_f – ω) = 4.

Substitute I = 4/5 and ω_f = 4 (from (2)):

(4/5)(4 – ω) = 4.

Solve for ω:

4 – ω = (4×5)/4 = 5 → ω = 4 – 5 = –1.

Thus the initial spin must be

ω = –1 rad/s.

Interpreting the sign: A negative value means that the sphere is spinning clockwise. (This is consistent with the fact that for pure rolling to the right one would need ω = –4; here the initial spin is “too little” for pure rolling and the collision “corrects” it.)

Summary of the Core (Minimal) Explanation:

The collision reverses the centre–of–mass speed so that v₍f₎ = –4 m/s.
Pure rolling on the floor after collision requires v₍f₎ + rω₍f₎ = 0, so ω₍f₎ = 4 rad/s.
The friction impulse changes the spin by:

I (ω₍f₎ – ω) = J_f.
With I = 4/5 and maximum friction impulse available = μJₙ = 4 (since Jₙ = 16), we have

(4/5)(4 – ω) = 4 ⟹ ω = –1 rad/s.

Answer:

The required initial angular speed is –1 rad/s (i.e. 1 rad/s clockwise).