Question

A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. If the rim of the hemisphere is kept horizontal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup
A. $\dfrac{{17}}{7}mg$
B. $18mg$
C. $\dfrac{{19}}{9}mg$
D. $20mg$

Answer 1

The normal force of the body will be the sum of forces acting in a downward direction. But to find the normal force we need to know the velocity of the sphere in the cup, due to its rolling motion. We can find it using the law of the conservation of energy for the sphere.
Formula used:
$N = mg + \dfrac{{m{v^2}}}{R}$
${\left( {K.E.} \right)_{rot}} = \dfrac{1}{2}I{\omega ^2}$

Complete answer:
In the question, they’ve asked us for the normal force acting on the sphere. Normal force ‘$N$’, being a contact force balances the weight and the driving force that keeps the sphere moving in the cup. They are mathematically given by,
$N = mg + \dfrac{{m{v^2}}}{R}$
Here,
$m$ is the mass of the sphere
$v$ is the velocity of the sphere
$R$ is the radius of the hemispherical cup
The velocity of the sphere is due to the rolling motion. It can be found as follows.
Let’s draw a rough sketch, for a better understanding and easier explanation.

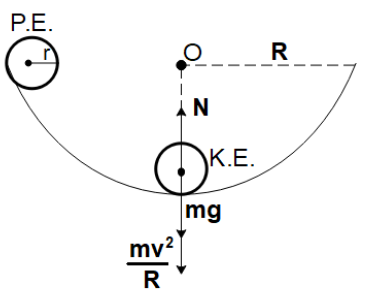
Initially, the sphere is on the rim, at a height of R from the ground. So, it will have a potential energy of
$P.E. = mgR$
Where,
$P.E.$ is the potential energy of the sphere
$m$ is the mass of the sphere
$g$ is the acceleration due to gravity
$R$ is the height of the sphere from the ground
Once the sphere reaches the bottom of the cup, it has rotational kinetic energy about its center of mass and translational kinetic energy due to rolling motion. So, the total kinetic energy of the sphere can be written as
${\left( {K.E.} \right)_T} = {\left( {K.E.} \right)_{rot}} + {\left( {K.E.} \right)_{trans}}$
The rotational kinetic energy of the sphere is given by
${\left( {K.E.} \right)_{rot}} = \dfrac{1}{2}I{\omega ^2}$
Where,
$I$ is the moment of inertia of the sphere
$\omega$ is the angular velocity of the sphere
As the sphere is rotating about its tangential axis, we have $I = \dfrac{2}{5}m{r^2}$ and the angular velocity can be written as $\omega = \dfrac{v}{r}$. Here, the $r$ indicates the radius of the sphere. Using these relations, rotational kinetic energy can be given by
\eqalign{ & {\left( {K.E.} \right)_{rot}} = \dfrac{1}{2}I{\omega ^2} \cr & \Rightarrow {\left( {K.E.} \right)_{rot}} = \dfrac{1}{2} \times \dfrac{2}{5}m{r^2} \times {\left( {\dfrac{v}{r}} \right)^2} \cr & \Rightarrow {\left( {K.E.} \right)_{rot}} = \dfrac{1}{5}m{v^2} \cr}
Similarly, the translational kinetic energy is given by ${\left( {K.E.} \right)_{trans}} = \dfrac{1}{2}m{v^2}$.
Substituting these values, we have the total kinetic energy of the sphere will
\eqalign{ & {\left( {K.E.} \right)_T} = {\left( {K.E.} \right)_{rot}} + {\left( {K.E.} \right)_{trans}} \cr & \Rightarrow {\left( {K.E.} \right)_T} = \dfrac{1}{5}m{v^2} + \dfrac{1}{2}m{v^2} \cr & \Rightarrow {\left( {K.E.} \right)_T} = \dfrac{7}{{10}}m{v^2} \cr}
From the law of conservation of energy, the potential energy changes into kinetic energy. Thus,
\eqalign{ & P.E. = {\left( {K.E.} \right)_T} \cr & \Rightarrow mgR = \dfrac{7}{{10}}m{v^2} \cr & \Rightarrow {v^2} = \dfrac{{10}}{7}gR \cr}
Now, the normal force of the sphere can be found by substituting this value, as
\eqalign{ & N = mg + \dfrac{{m{v^2}}}{R} \cr & \Rightarrow N = mg + \dfrac{{m \times \dfrac{{10}}{7}gR}}{R} \cr & \Rightarrow N = mg + \dfrac{{10}}{7}mg \cr & \therefore N = \dfrac{{17}}{7}mg \cr}

Therefore, the correct option is A.

Note:
One can misjudge that normal force is always equal to the weight. The Normal force is a supporting force one the object against a stable object. In our problem, the ball or sphere is moving in a circular motion with some velocity. So, the normal force will not just counteract weight but also force due to circular motion, towards the center.