Question

A solid sphere of mass m is lying on a rough horizontal surface. The coefficient of friction between the ground and sphere is $\mu .$ The maximum values of F, so that the sphere will not slip, is equal to

A.)$\dfrac{7}{5}\mu mg$
B.)$\dfrac{4}{7}\mu mg$
C.)$\dfrac{5}{7}\mu mg$
D.)$\dfrac{7}{2}\mu mg$

Answer 1

Hint- In this situation it all depends on the frictional force and the torque of force acting on the sphere, which is the concept of rotational mechanics . Thus we need to compare by equations of force and then apply the condition for slipping of the sphere.

Complete step-by-step answer:
For sphere not to slip, its frictional force must be greater than the net force acting on the sphere in horizontal direction because if the net force exceeds the friction then the body starting slipping .which is shown below:

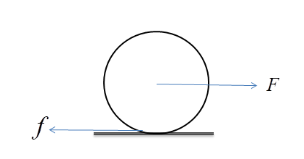
Let F be the force, R be the radius and I be the moment of inertia.

$\alpha$ is the rotational acceleration
$\mu$ is the coefficient of friction.

As the sphere is rolling we can apply the torque equation about the point of contact P.

$\Rightarrow FR = {I_P}\alpha \\\ \Rightarrow FR = \left( {\dfrac{7}{5}M{R^2}} \right)\alpha \\\ \Rightarrow R\alpha = \dfrac{{5F}}{{7M}} = a \\\$

Now applying the equation for translatory motion

$F - f = Ma$

Substituting the value of acceleration in the above equation

$F - f = M \times \dfrac{{5F}}{{7M}} \\\ f = \dfrac{2}{7}F \\\$

The condition for no slipping is

$f \leqslant \mu mg$

Now, substituting the value of the frictional force in terms of Force in the above condition to find the minimum value of force required to move the body without slipping.

$\dfrac{2}{7}F \leqslant \mu mg \\\ F \leqslant \dfrac{7}{2}\mu mg \\\$

Hence the correct option is D.

Note- Rolling without slipping means there is a friction force acting on the wheel at the contact point P. This friction force prevents slipping. In this instance the friction is known as static friction since there is no relative sliding between the wheel and surface at the contact point P.