Question

A solid sphere of mass $M$ and radius $R$ is placed on a rough horizontal surface. A horizontal force $F$ is applied to the sphere at a height $h(0 \le h \le R)$ from the centre as shown in figure. If the sphere rolls without slipping, then choose correct options.

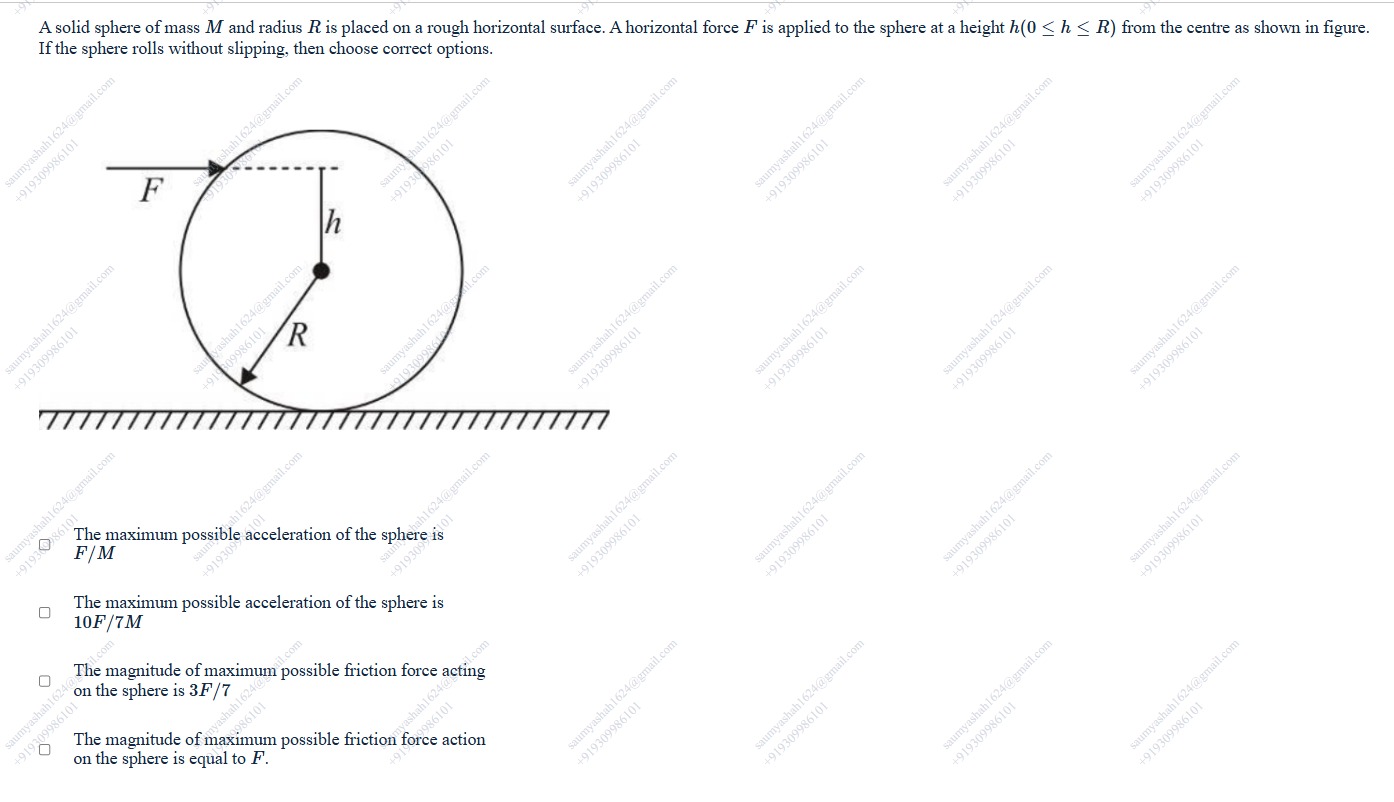
• A. The maximum possible acceleration of the sphere is $F/M$
• B. The maximum possible acceleration of the sphere is $10F/7M$
• C. The magnitude of maximum possible friction force acting on the sphere is $3F/7$
• D. The magnitude of maximum possible friction force action on the sphere is equal to $F$.

Answer 1

Answer: (B), (C)

The maximum possible acceleration of the sphere is $10F/7M$, The magnitude of maximum possible friction force acting on the sphere is $3F/7$

Answer 2

The forces acting on the solid sphere are the applied force $F$ at height $h$ above the center, the gravitational force $Mg$ at the center, the normal force $N$ at the point of contact, and the static friction force $f$ at the point of contact.

For vertical equilibrium, $N - Mg = 0$, so $N = Mg$. For horizontal motion, $F - f = Ma$, where $a$ is the linear acceleration of the center of mass. For rotational motion about the center of mass, the torque is due to $F$ and $f$. The torque due to $F$ is $Fh$ (clockwise). Let's assume friction $f$ acts to the left, then the torque due to $f$ is $fR$ (clockwise). The net torque is $Fh + fR = I\alpha$, where $I = \frac{2}{5}MR^2$ is the moment of inertia of a solid sphere about its center and $\alpha$ is the angular acceleration. For rolling without slipping, $a = R\alpha$. So $\alpha = a/R$. The torque equation becomes $Fh + fR = \frac{2}{5}MR^2 \left(\frac{a}{R}\right) = \frac{2}{5}MRa$. We have the equations:

1. $F - f = Ma$
2. $Fh + fR = \frac{2}{5}MRa$

From (1), $f = F - Ma$. Substitute into (2): $Fh + (F - Ma)R = \frac{2}{5}MRa$ $Fh + FR - MaR = \frac{2}{5}MRa$ $F(h+R) = MaR + \frac{2}{5}MRa = \left(R + \frac{2}{5}R\right)Ma = \frac{7}{5}MRa$ The acceleration is $a = \frac{5F(h+R)}{7MR}$.

The friction force is $f = F - Ma = F - M \left(\frac{5F(h+R)}{7MR}\right) = F - \frac{5F(h+R)}{7R} = \frac{7FR - 5Fh - 5FR}{7R} = \frac{2FR - 5Fh}{7R} = \frac{F(2R - 5h)}{7R}$.

The condition for rolling without slipping is $|f| \le \mu_s N = \mu_s Mg$. So, $\left|\frac{F(2R - 5h)}{7R}\right| \le \mu_s Mg$.

We are asked for the maximum possible acceleration and maximum possible friction force if the sphere rolls without slipping. This means we consider the range of $h$ from $0$ to $R$.

The acceleration $a = \frac{5F(h+R)}{7MR}$ is an increasing function of $h$. Since $0 \le h \le R$, the maximum value of $a$ occurs at $h=R$. Maximum acceleration $a_{max} = \frac{5F(R+R)}{7MR} = \frac{5F(2R)}{7MR} = \frac{10F}{7M}$. This maximum acceleration is possible if rolling without slipping can occur at $h=R$.

At $h=R$, the friction force is $f = \frac{F(2R - 5R)}{7R} = \frac{F(-3R)}{7R} = -\frac{3F}{7}$. The negative sign indicates that the friction force is to the right, opposite to our initial assumption. The magnitude of the friction force is $|f| = \frac{3F}{7}$. For rolling without slipping to occur at $h=R$, the required friction force must be within the limit of static friction: $\frac{3F}{7} \le \mu_s Mg$. If this condition is met, then the maximum acceleration is indeed $\frac{10F}{7M}$.

Now consider the magnitude of the friction force $|f| = \left|\frac{F(2R - 5h)}{7R}\right|$. As $h$ varies from $0$ to $R$, the value of $2R - 5h$ varies from $2R$ (at $h=0$) to $2R - 5R = -3R$ (at $h=R$). The range of $2R - 5h$ is $[-3R, 2R]$. The range of $|2R - 5h|$ is $[0, \max(|-3R|, |2R|)] = [0, 3R]$. The range of $|f| = \frac{F}{7R}|2R - 5h|$ is $\left[0, \frac{F}{7R}(3R)\right] = \left[0, \frac{3F}{7}\right]$. The maximum magnitude of the friction force required for rolling without slipping, as $h$ varies from $0$ to $R$, is $\frac{3F}{7}$. This occurs at $h=R$.

Let's check the options: Option 1: The maximum possible acceleration of the sphere is $F/M$. Incorrect. Option 2: The maximum possible acceleration of the sphere is $10F/7M$. Correct, provided rolling without slipping is possible at $h=R$. Option 3: The magnitude of maximum possible friction force acting on the sphere is $3F/7$. This is the maximum magnitude of the required static friction force for rolling without slipping over the range of $h$. Correct. Option 4: The magnitude of maximum possible friction force action on the sphere is equal to $F$. Incorrect.

The question asks for correct options. Options 2 and 3 are correct statements about the maximum possible acceleration and the magnitude of maximum possible friction force required for rolling without slipping, assuming that the coefficient of static friction is sufficient to allow rolling without slipping for all $h \in [0, R]$ or at least at $h=R$. If the coefficient of static friction is not large enough, then rolling without slipping might not be possible for all values of $h$. However, the question asks "If the sphere rolls without slipping", implying that we are considering the scenario where the conditions for rolling without slipping are met. In this context, the maximum possible acceleration is the maximum value of $a$ over the range of $h$ for which rolling without slipping is possible. Similarly for the friction force. The maximum values of $a$ and $|f|$ are obtained at $h=R$, and these values are $\frac{10F}{7M}$ and $\frac{3F}{7}$, respectively.