Question

A solid sphere of mass M and radius R has a spherical cavity of radius $\frac{R}{2}$ such that the centre of cavity is at distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational pull between the sphere and the point mass m is:

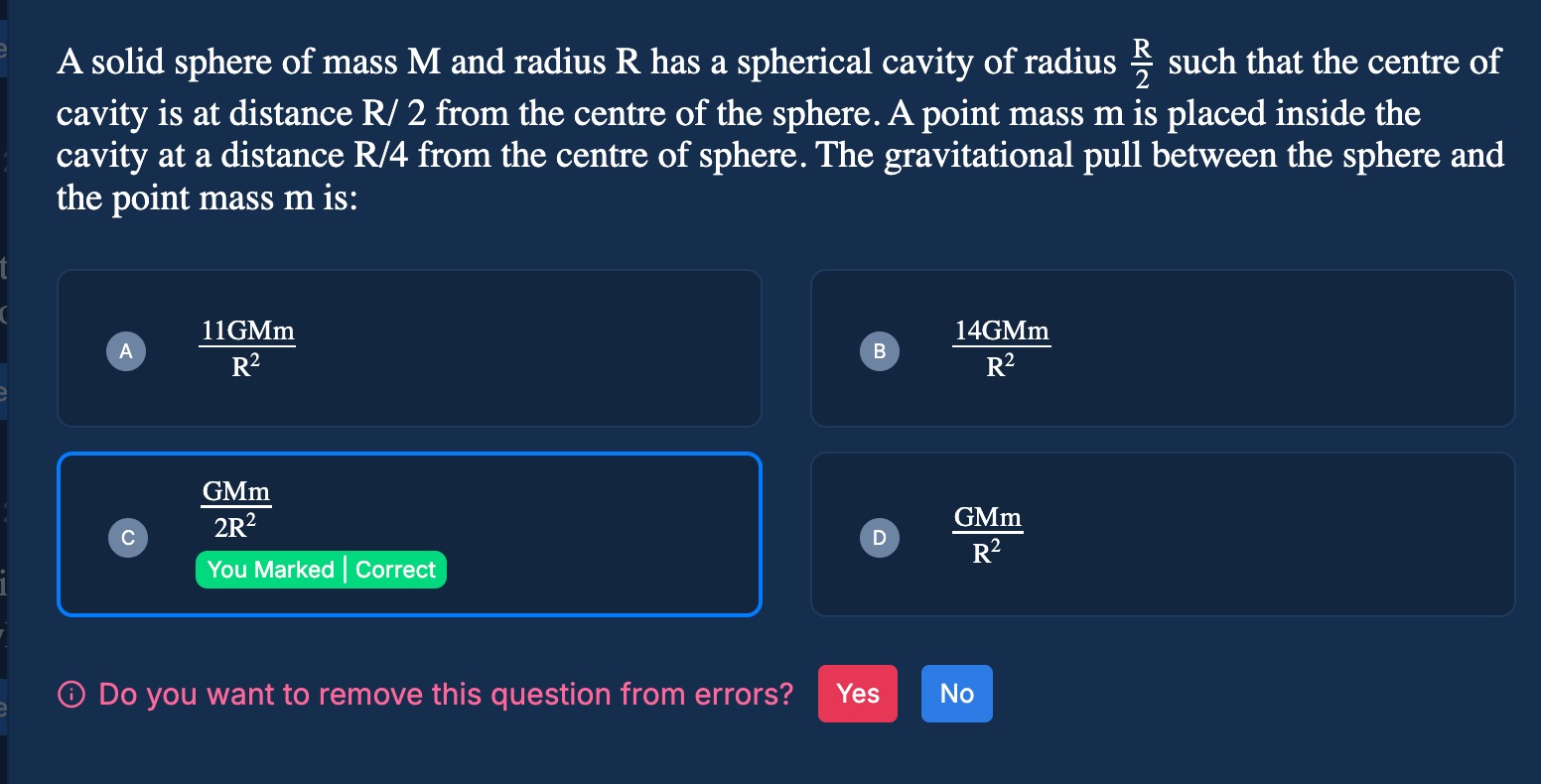
• A. fraction with numerator 11GMm and denominator R squared
• B. fraction with numerator 14GMm and denominator R squared
• C. fraction with numerator GMm and denominator 2R squared
• D. fraction with numerator GMm and denominator R squared

Answer 1

Answer: (C)

$\dfrac{GMm}{2R^2}$

Answer 2

Solution Explanation:
Represent the sphere with a cavity as a superposition of a full sphere (mass M) and a "negative mass" cavity (mass M/8). For a uniform sphere, the gravitational field inside a sphere at a distance r from the center is
  $g = \dfrac{GM\,r}{R^3}$.

1. Full sphere contribution:
    For the point mass at distance $r_1=\dfrac{R}{4}$ from the center,
     $g_1 = \dfrac{GM}{R^3}\cdot \dfrac{R}{4} = \dfrac{GM}{4R^2}$ (directed toward the center).

2. Cavity contribution:
    The cavity (negative mass $-\frac{M}{8}$) is centered at $\dfrac{R}{2}$ from the center. The distance from the cavity’s center to the point mass is
     $r_2 = \left|\dfrac{R}{4} - \dfrac{R}{2}\right| = \dfrac{R}{4}$.
    Inside a uniform sphere, the field is
     $g = \dfrac{G\,(\text{mass}) \,r}{a^3}$, with $a=\dfrac{R}{2}$.
    Thus, for the cavity,
     $g_2 = \dfrac{G\,(M/8)}{(R/2)^3}\cdot \dfrac{R}{4} = \dfrac{G(M/8)}{R^3/8}\cdot \dfrac{R}{4} = \dfrac{GM}{4R^2}$.
    Because the mass is removed (negative), the effective field is reversed. Since the point mass lies between the center of the sphere and the cavity center, both contributions act in the same (inward) direction.

3. Net gravitational field:
    $g_{\text{net}} = g_1 + g_2 = \dfrac{GM}{4R^2} + \dfrac{GM}{4R^2} = \dfrac{GM}{2R^2}$.

4. Gravitational Force on m:
    $F = m \, g_{\text{net}} = \dfrac{GMm}{2R^2}$.

Answer:
$\boxed{\dfrac{GMm}{2R^2}}$ (Option C)