Question

A solid sphere of mass is placed on a rough surface having coefficient of friction $\mu = 0.1$. A constant force $F = 7\,{\text{N}}$ is applied along a line passing through the centre of the sphere as shown in the figure. The value of frictional force on the sphere is

A. $1\,{\text{N}}$
B. $2\,{\text{N}}$
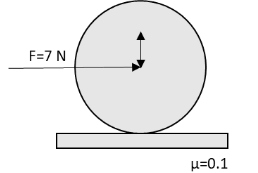
C. $3\,{\text{N}}$
D. $7\,{\text{N}}$

Answer 1

Determine the torque acting on the cylinder due to frictional force acting on it. Substitute value of torque in terms of angular acceleration in this formula. Apply Newton’s second law of motion to the cylinder in horizontal direction and substitute value of angular acceleration in this derivation and determine the frictional force.

Formulae used:
The expression for Newton’s second law of motion is
${F_{net}} = ma$ …… (1)
Here, ${F_{net}}$ is net force on the object, $m$ is mass of the object and $a$ is acceleration of the object.
The torque $\tau$ acting on an object is
$\tau = I\alpha$ …… (2)
Here, $I$ is the moment of inertia of an object and $\alpha$ is the angular acceleration of the object.
The torque $\tau$ acting on an object due to force $F$ is
$\tau = Fr$ …… (3)
Here, $r$ is the perpendicular distance between the point of action of the force and centre of the torque.
The acceleration $a$ of an object is
$a = R\alpha$ …… (4)
Here, $R$ is the radius of the circular path and $\alpha$ is angular acceleration of the object.

Complete step by step answer:
We have given that a solid sphere of mass is placed on a rough surface having coefficient of friction $\mu = 0.1$. A constant force $F = 7\,{\text{N}}$ is applied along a line passing through the centre of the sphere as shown in the figure. The free body diagram of the given sphere is as follows:

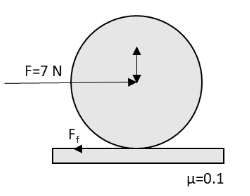
Due to the spherical shape of the cylinder, the cylinder will have translational as well as rotational motion. The torque due to the frictional force is
$\tau = {F_f}R$
Here, $R$ is the radius of the cylinder.
Substitute $I\alpha$ for $\tau$ in the above equation.
$I\alpha = {F_f}R$
$\Rightarrow \alpha = \dfrac{{{F_f}R}}{I}$
Here, $I$ is a moment of inertia of the solid sphere.
Substitute $\dfrac{2}{5}m{R^2}$ for $I$ in the above equation.
$\Rightarrow \alpha = \dfrac{{{F_f}R}}{{\dfrac{2}{5}m{R^2}}}$
$\Rightarrow \alpha = \dfrac{{5{F_f}}}{{2mR}}$

Apply Newton’s second law of motion to the cylinder in the horizontal direction.
$F - {F_f} = ma$
Substitute $R\alpha$ for $a$ in the above equation.
$F - {F_f} = mR\alpha$
Substitute $\dfrac{{5{F_f}}}{{2mR}}$ for $\alpha$ in the above equation.
$F - {F_f} = mR\dfrac{{5{F_f}}}{{2mR}}$
$\Rightarrow F = \dfrac{{5{F_f}}}{2} + {F_f}$
$\Rightarrow F = \dfrac{{7{F_f}}}{2}$
$\Rightarrow F = 3.5{F_f}$
$\Rightarrow {F_f} = \dfrac{F}{{3.5}}$
Substitute $7\,{\text{N}}$ for $F$ in the above equation.
$\Rightarrow {F_f} = \dfrac{{7\,{\text{N}}}}{{3.5}}$
$\therefore {F_f} = 2\,{\text{N}}$
Therefore, the value of frictional force is $2\,{\text{N}}$.

Hence, the correct option is B.

Note: The students may think that why acceleration is positive when applied to Newton's second law as it may be negative if the frictional force is greater than force F. We have considered the solid cylinder is moving in the right direction due to the force applied to the centre of the cylinder. Hence, the direction of acceleration of the cylinder is toward the right and hence it is positive.