Question

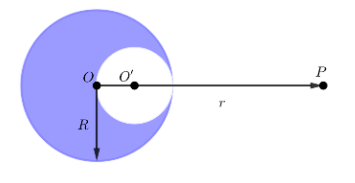
A solid sphere of lead has a mass M and radius R. A spherical hollow is dug out from it (see figure below). Its boundary passes through the center and also touches the boundary of the solid sphere. Deduce the gravitational force on a mass m placed at P, which is at a distance r from O along the line joining the centres.

Answer 1

We have a solid sphere and a hollow sphere dug out from it. As we need to find the gravitational force on mass m due to the sphere. So, firstly find the gravitational force due to the solid sphere and the hollow sphere separately. Then, subtract the gravitational force due to the hollow sphere from the gravitational force due to the solid sphere.

Formula used:
$F=\dfrac{GMm}{{{r}^{2}}}$
where F is the gravitational force acting between two bodies of masses M and m separated by a distance r and G is the gravitational constant.

Complete step by step answer:
The center of mass of the solid and hollow spheres is assumed to be their centers O and O’ respectively.
The force acting on a mass m placed at P at a distance r away from the center of the solid sphere is
${{F}_{s}}=\dfrac{GMm}{{{r}^{2}}}$
The solid sphere has mass M and radius R. Let M’ be the mass of the spherical hollow of radius $\dfrac{R}{2}$ that has been dug out. Assuming the density remains uniform throughout

& \dfrac{M}{\dfrac{4}{3}\pi {{R}^{3}}}=\dfrac{M'}{\dfrac{4}{3}\pi {{\left( \dfrac{R}{2} \right)}^{3}}} \\\ & M'=\dfrac{M}{8} \\\ \end{aligned}$$ The force acting on a mass m placed at P at a distance $\left( r-\dfrac{R}{2} \right)$ away from the center of the hollow sphere is, ${{F}_{h}}=\dfrac{GMm}{8{{\left( r-\dfrac{R}{2} \right)}^{2}}}$ Since ${{F}_{s}}$ and ${{F}_{h}}$ point in the same direction along with OP. Therefore, the net force acting on the mass m is $\begin{aligned} & F={{F}_{s}}-{{F}_{h}} \\\ & =\dfrac{GMm}{{{r}^{2}}}-\dfrac{GMm}{8{{\left( r-\dfrac{R}{2} \right)}^{2}}} \\\ & =\dfrac{GMm}{{{r}^{2}}}\left[ 1-\dfrac{1}{8{{\left( 1-\dfrac{R}{2r} \right)}^{2}}} \right] \end{aligned}$ **Additional information:** Gravity is the weakest of the four fundamental interactions in the universe. It is 1038 times weaker than the strong interaction, 1036 times weaker than the electromagnetic interaction, and 1029 times weaker than the weak interaction. It has only macroscopic effects in the universe. Consequently, it does not affect subatomic particles but is responsible for the formation, shape, and orbits of astronomical bodies. **Note:** While finding the gravitational force by both the spheres, be careful to identify the mass as well as the radius of the hollow sphere. Also, be careful with the distance between the center of the hollow sphere and the mass m.