Question

A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction is $\mu$ ) with speed of centre $u$ . It collides inelastically with a smooth vertical wall at a certain moment, the coefficient of restitution being $\dfrac{1}{2}$ the time when the sphere will start pure rolling is?

Answer 1

First, we will find the angular velocity after using formula we will determine external torque and then we will find the angular as well as linear velocity and then applying the properties for pure rolling motion and substituting all the values in the equation and solving for the time taken and hence, we will get the required solution.

Formula used:
$\omega = \alpha t$
$\tau = I\alpha$
Where,
$\omega$ is the change in angular velocity,
$\tau$ is the torque,
$I$ is the moment of inertia
$\alpha$ is angular velocity and
$t$ is the time.

Complete step by step solution:

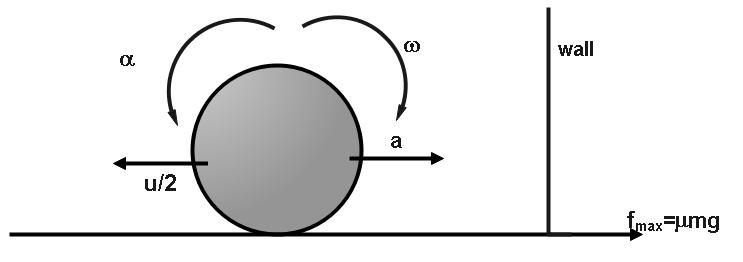
We know that when pure rolling occurs, we can write,
$\omega = \dfrac{u}{r}$ .
According to the question,
The coefficient of kinetic friction is $\mu$
And it is given that, the coefficient of restitution being $\dfrac{1}{2}$ the time when the sphere will start pure rolling. So, we can say that after the collision occurs the velocity of the sphere will be $\dfrac{u}{2}$ in the opposite direction.
Therefore, the new angular velocity will be, $\omega = - \dfrac{u}{r}$ taking a positive direction as clockwise.
Now, the external torque acting because of frictional force,
Where,
$f$ is the frictional force,
$\alpha$ is the angular acceleration and
$I$ is the moment of inertia.
So, we can write, $r \times \mu mg = \dfrac{2}{5}m{r^2}\alpha$
Therefore,
$\alpha = \dfrac{{5\mu g}}{{2r}}$
And resolving the linear force we can see diagram,
$f = ma \\\ \Rightarrow \mu mg = ma \\\ \Rightarrow \mu g = a \\\$
And we know that for pure rolling $v = r\omega$ -----(1)
Now let us assume that after time $t$ angular velocity will be $\omega '$
So, we can write that,
$\omega ' = \omega + \alpha t$
And the linear velocity after time $t$ will be, $v = \dfrac{u}{2} - at$ .
Now, putting the value of $v$ , $\omega '$ $\alpha$ and $a$ in equation (1) and solving for $t$ .
$v = r\omega \\\ \Rightarrow \dfrac{u}{2} - at = r\left( {\omega + \alpha t} \right) \\\ \Rightarrow \dfrac{u}{2} - \mu gt = r\left( { - \dfrac{u}{r} + \dfrac{{5\mu g}}{{2r}}t} \right) \\\$
Further solving the equation,

$$\Rightarrow \dfrac{u}{2} - \mu gt = r\left( { - \dfrac{u}{r} + \dfrac{{5\mu g}}{{2r}}t} \right) \\\ \Rightarrow \dfrac{{u - 2\mu gt}}{2} = r\left( {\dfrac{{5\mu gt}}{{2r}} - \dfrac{u}{r}} \right) \\\$$

Now, taking common $r$ and solving,

$$\Rightarrow \dfrac{{u - 2\mu gt}}{2} = \dfrac{{5\mu gt - 2u}}{2} \\\ \Rightarrow t = \dfrac{{3u}}{{7\mu g}} \\\$$

Hence, the required time when the sphere will start pure rolling is $\dfrac{{3u}}{{7\mu g}}$.

Note:
When a body's rotation and translation motions are coupled, we call it rolling. Slipping motion is defined as an object's ability to slide across a surface. A person's body can roll without slipping or with slippage.
Conditions for pure rolling:
When there is no resistance to the motion, it is called pure rolling. Friction is required to get the ball moving, but it is no longer required once it has started rolling. Pure rolling occurs when the rolling body's point of lowest contact with the ground remains stationary and the body is designed to rotate around this point of contact.