Question
Question: A solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity v...
A solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity v m/s. If it is to climb the inclined surface then v should be
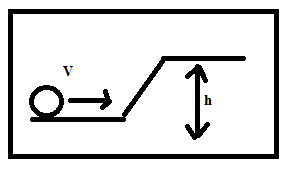
A. ≥710gh
B. ≥2gh
C. 2gh
D. 710gh
Solution
Hint: Use conservation energy principle to solve this problem. That is total energy after climbing at height h. Assume final velocity to be zero for obtaining the minimum value of velocity. Do not forget potential energy.
Complete step-by-step answer:
In general for any object total energy is the sum of Kinetic and Potential energy.
So, for this problem
According to conservation law of energy we can equate total initial energy and total final energy.
(Total energy)initial=(Total energy)final
(K.E.)i+(P.E.)i=(K.E.)f+(P.E.)f
Where
K.E. = kinetic energy
P.E = potential energy
(K.E.)i+(P.E.)i=(K.E.)f+(P.E.)f …. 1
(K.E.)i: As the sphere is rolling it will have both translational energy and rotational energy.
As it is rolling
v=rw
w=rv …… 2
(K.E.)i=21mv2+21mw2
=21mv2+52mr2(rv)2 [I solid sphere =52mr2]
=21mv2+5mv2
=(K.E.)i=107mv2 .... 3
(K.E.)f: As the sphere will stop translating, that is final velocity is zero for obtaining the minimum velocity.
(K.E.)f=21mv2+21Iw2
=21m(0)2+21I(0)2
(K.E.)f=0 ….. 4
Change in potential energy (P.Ef−P.Ei)
As we know that potential energy cannot be defined at a particular time and position. It can be calculated as a change in quantity.
So,
(P.Ef−P.Ei)=mg(h)
(P.E)f−(P.E)i=mgh
Using equation 1
(K.E.)i=(K.E.)f+((P.E)f−(P.E)i
107mv2=0+mgh
v=710gh
Minimum value of velocity to reach a height h=710gh
v≥vminimum
v≥710gh
Hence option A.
Note: This can be done using this change in potential energy = change in kinetic energy. Conservation of energy principle needs to be remembered to solve this kind of problem. In this question, it was given that the surface is frictionless. So we didn't consider the frictional force. If the surface will not be frictionless, then we have to consider the frictional force.
