Question

A solid sphere and hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ${{\omega }_{0}}$. Once the pure rolling starts let ${{v}_{1}}$ and ${{v}_{2}}$ be the linear speeds of their centres of mass. Then

& \text{A}\text{. }{{v}_{1}}={{v}_{2}} \\\ & \text{B}\text{. }{{v}_{1}}>{{v}_{2}} \\\ & \text{C}\text{. }{{v}_{1}}<{{v}_{2}} \\\ & \text{D}\text{. Data insufficient} \\\ \end{aligned}$$

Answer 1

Hint : Frictional force drives the rotating object. When the velocity of the lowermost point is such that it satisfies a specific condition, it starts pure rolling motion. The frictional force stays the same throughout the motion and this force is responsible for the velocity of the rotating object.
Formula Used:
Acceleration due to a force is given by,
f=ma
The relation between torque and angular acceleration is,
$\Gamma =I\alpha$

$v=u+at$
$\omega ={{\omega }_{0}}+\alpha t$

Complete step by step answer:
Let’s look at the following diagram and understand the motion:

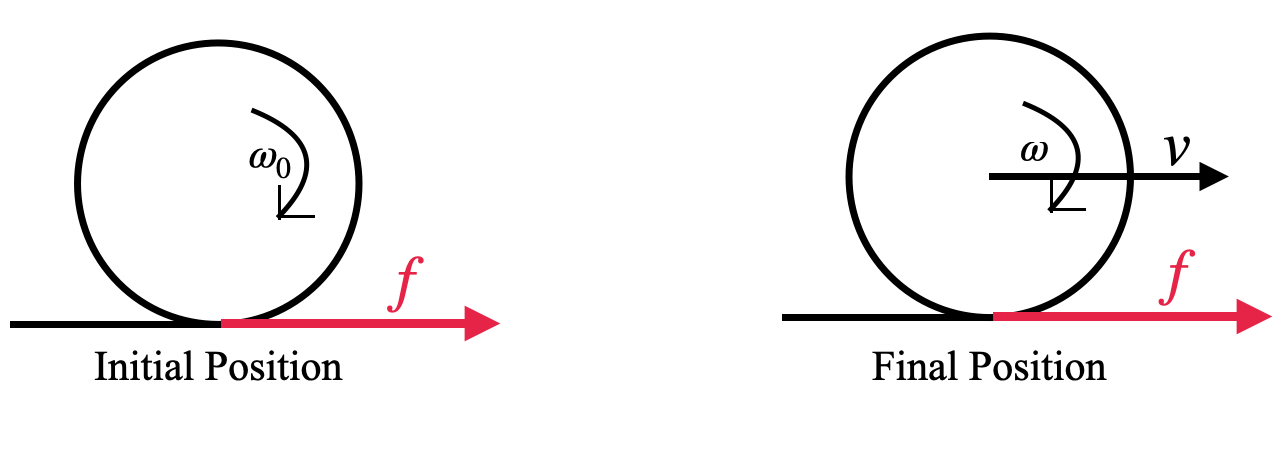
Initially the object is rotating at an angular velocity = ${{\omega }_{0}}$
The frictional force f starts acting in the forward direction.

This does two things-
(i) Increase the linear velocity
(ii) Decrease the angular velocity

When the following condition is met, the lowermost point starts behaving like a fixed point with respect to the ground. Then pure rolling starts.
$v=\omega r$

We can write,
$f=ma$
$\Rightarrow a=\dfrac{f}{m}$

Where,
f is the frictional force
m is the mass of the object
a is the acceleration of the object.

Let’s assume that the object takes ‘t’ to reach pure rolling condition.

Hence, the velocity of the object will be,
$v=0+\left( \dfrac{f}{m} \right)t$
$\Rightarrow t=\dfrac{mv}{f}$

Now, the frictional force also gives an opposite torque. Torque is given by,
$\Gamma =fr$
Hence, we can write,
$fr=I\alpha$
Where,
$I$ is the moment of inertia of the object

So, the angular acceleration is given by,
$\alpha =\dfrac{fr}{I}$

So, we can write,
$\omega ={{\omega }_{0}}-\left( \dfrac{fr}{I} \right)t$
$\Rightarrow \dfrac{v}{r}={{\omega }_{0}}-\left( \dfrac{fr}{I} \right)\left( \dfrac{mv}{f} \right)$
$\Rightarrow v\left( 1+\dfrac{m{{r}^{2}}}{I} \right)={{\omega }_{0}}r$
$\Rightarrow v=\dfrac{{{\omega }_{0}}r}{\left( 1+\dfrac{m{{r}^{2}}}{I} \right)}$

Hence, the velocity of the particle in terms of moment of inertia is given by,
$v=\dfrac{{{\omega }_{0}}r}{\left( 1+\dfrac{m{{r}^{2}}}{I} \right)}$...............(1)

Moment of inertia of solid sphere is given by,
${{I}_{solid}}=\dfrac{2}{5}m{{r}^{2}}$

Moment of inertia of hollow sphere is given by,
${{I}_{hollow}}=\dfrac{2}{3}m{{r}^{2}}$

Hence,
${{I}_{hollow}}>{{I}_{solid}}$

So, from equation (1) we can say that,
${{v}_{2}}>{{v}_{1}}$

So, the correct option is - (C).

Note :
We can compare the moment of inertia of two similar objects without looking at the actual values. For example, if we have to compare the moment of inertias of solid sphere and hollow sphere, we can compare the distribution of mass. If the mass is more towards the periphery of the object, then the moment of inertia will be more. So, the moment of inertia of the hollow sphere is more than the solid sphere.