Question
Question: A solid non-conducting sphere of radius \(R\), having a spherical cavity of radius \(\dfrac{R}{2}\) ...
A solid non-conducting sphere of radius R, having a spherical cavity of radius 2R as shown, carries a uniformly distributed charge q. The electric field at the centre of the cavity is:
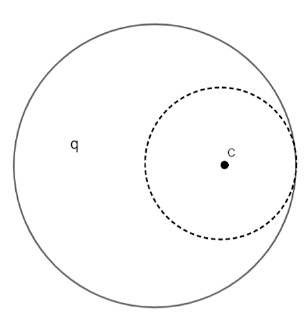
Solution
From the Gauss Law of Electrostatics we can find out the electric field.The electric field inside a non-conducting sphere is 0. So, we have to find out the electric field only of the cavity. The electric field of the cavity is the same as the electric field at the surface of any sphere. Since, the cavity is in the positive direction of the X-axis so we will consider the outcome to be a positive value.
Complete step by step answer:
From the Gauss Law of Electrostatics we know,
∮E.dS=ε0q−−−−−(1) where E is the electric field, dS is the enclosed surface area, q is the charge enclosed.
In the given figure O is the centre. Let A be any point on the surface. The charge enclosed in the non-conducting sphere is=0. So, the electric field here is also 0. We have to just find out the electric field of the cavity. According to the given question,
Charge enclosed by the sphere=q.
The radius of the cavity is given as 2R.
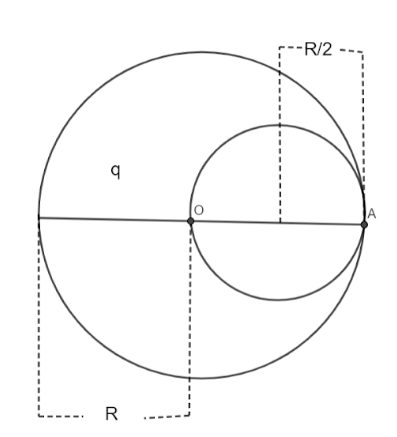
Let the volume charge density over radius R be ρ.
q=ρ×34πR3
So, the charge q′ over radius 2R is q=ρ×34π(2R)3=ρ6πR3
dS=enclosed area of the cavity=4π(2R)2=πR2
Substituting these values in equation (1) we get,
E.dS=εq′
⇒E=πR2ε0ρ6πR3 ∴E=6ε0ρR
Thus now we get the electric field E=6ε0ρR.
Note: Gauss Law is applicable in many cases as it is shown here. The electric field inside both a hollow sphere and a non-conducting sphere is 0. But the electric field inside a conducting sphere is not 0 as the charge does not reside outside the sphere.
