Question

A solid metal cube of edge length 2 cm is moving in a positive $y$ direction at a constant speed of 6 m/s. There is a uniform magnetic field of 0.1 T in the positive $z$ - direction. The potential difference between the two faces of the cube perpendicular to the $x$ - axis is:
A. 6 mV
B. 1 mV
C. 12 mV
D. 2 mV

Answer 1

Here, we can use the formula for emf of a moving body.
Formula used:
${\text{E}} = {\text{B}}lv$

Complete step-by-step answer:
Let us consider the above given problem
Given that a solid metal cube has an edge length of 2 cm that moves in a positive direction at a constant speed of 6 m/s.
Let $l$ be the edge length of the cube, B be the uniform magnetic field and $v$ be the constant speed of the solid metal cube.
The uniform magnetic field of 0.1 T is in the positive $z$ - direction as shown in the diagram.

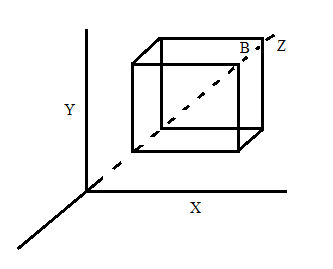
As the metal cube is moving the emf is generated which is nothing but the potential difference between the two faces of the cube perpendicular to the $x$ - axis.
Let us consider the formula for emf, ${\text{E}} = {\text{B}}lv$
We can now substitute the values B= 0.1 T,$l = {\text{2 cm = 2 }} \times 10_{}^{ - 2}{\text{ m}}$
$\Rightarrow {\text{E = 0}}{\text{.1 }} \times {\text{ 2}} \times 10_{}^{ - 2}{\text{ }} \times {\text{ 6}}$
$\Rightarrow {\text{E = 1}}{\text{.2 }} \times 10_{}^{ - 2}$
$\Rightarrow {\text{E = 12 }} \times 10_{}^{ - 3}{\text{ V}}$ $\Rightarrow {\text{E = 12mV}}$

Therefore (C) =12 mV is the required answer.

Additional information:
EMF stands for Electro-Motive Force.
EMF is defined as the energy supplied by a cell to circulate unit charge once round the complete circuit.
EMF is not a force but represents the energy spent per unit charge.
Whereas, the energy spent by the source of emf in circulating unit charge through external resistance is called a potential difference of the cell.
We measure the potential difference across the cell terminal when the cell is connected in the circuit or some current is drawn from the cell.
The unit of EMF and a potential difference is volt.
Note:
The direction of velocity and magnetic field should be taken care of while calculating the emf.
The value of emf E is positive as the magnetic field and velocity are acting along positive z and y directions respectively.